 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: Jun 2013
Posts: 10
Rep Power: 13  |
Hello all,
I was trying to implement 2-pt spatial velocity correlation to my data (ensembled averaged pulsatile flow through the pipe) but it seems like I am getting lost in the process. Here is what I understand, normalized autocorrelation function is defined as R(x,r)=<Vi'(x)Vi'(x+r)>/sqrt(<Vi'(x)^2>, <>-ensemble average. The velocity I am interested in is in streamwise direction and is represented by an NxM matrix, where V(1:N)-velocity change in radial direction, V(1:M) velocity change in a streamwise direction ("pipe flow"). Here ' -s a fluctuation component of the velocity. If fix my origin for 2-point spatial velocity correlation at x=x0, along the centerline of the pipe, in order for me to get Rii, do I sweep from x0 to xM by incrementing r between successive velocity values along the centerline of the pipe, i.e. R(1) = <Vi'(x)Vi'(x+r)>/sqrt(<Vi'(x)^2>, R(2) = <Vi'(x)Vi'(x+2r)>/sqrt(<Vi'(x)^2>, ..., R(M) = <Vi'(x)Vi'(x+Mr)>/sqrt(<Vi'(x)^2>? With this approach, the graph of R vs r does not look right, it cascades down from 1 to 0, oscillates a bit near 0 on the negative side of 0, and then shoots back to 1.6 and oscillates there. I guess I am missing something here. If somebody has experience with this type of calculations and can point out where I am off in my assumptions, I would greatly appreciate it. Thanks! |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
I am not sure to get exactly your question, however when you fix x=x0 then: R(x0,r)=<Vi'(x0)Vi'(x0+r)>/sqrt(<Vi'(x0)^2> = F(r) is a function only of the separation lenght r. Therefore you have to compute the function for each r. Why are you computing terms like R(M) = <Vi'(x)Vi'(x+Mr)>/sqrt(<Vi'(x)^2 ? |
||
|
|

|
||
|
|
|
#3 |
|
New Member
Join Date: Jun 2013
Posts: 10
Rep Power: 13  |
Hi Filippo,
Thank you for the reply! What you wrote are exactly two steps that I understand and confused about. Let me try to explain. at x=x0, I do calculate R(x0,r), the way you mentioned, only for V(x0,y0), where y0 is in the centerline of the pipe. I think my problem is with r. I treated r as a distance x0 and x0+dx, where dx is a distance between grid points. In order to get plot R(x0,r) vs. r I calculated: [<Vi'(x0)Vi'(x0+r)>/sqrt(<Vi'(x0)^2>, <Vi'(x0)Vi'(x0+2r)>/sqrt(<Vi'(x0)^2>, ..., <Vi'(x0)Vi'(x0+Mr)>/sqrt(<Vi'(x0)^2>] for [r, 2r, ..., Mr] I guess this is where I am getting it all wrong? I attached a sample image of what I am doing, maybe that would help to identify where I am wrong in my calculations? Basically, I only use yellow points for my calculation and vary r from r=r to r=mr to get a dependence of R(r) vs r. Would that be a correct approach?  Thank you in advance! |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
ok, I see... therefore:
1) you have the separation variable r sampled on the x-direction grid, r(i)=i*dx, i=1,...,M-1, note that r(M-1)=(M-1)dx; 2) what about the third dimension? 3) are you interested in the correlation or in the coefficient of correlation? you are actually computing the last one 4) is your case homogeneous? it would be independent from the choice of x0 |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Join Date: Jun 2013
Posts: 10
Rep Power: 13  |
I would say I am interested in both. Let me explain why:
I wanted to calculate coefficient of correlation so I can see how it declines over streamwise direction, which, if I understand correctly, can be translated to the correlation of the eddies in the turbulent flow. I think by comparing few phases of the flow, the eddies formed in various phases will change in size and structure, which should be reflected by the different correlation coefficient. I hope I understand that correctly. Regarding 2pt correlation, I wanted to use it to calculate a 1D wavenumber spectra, as FFT for 2pt correlation. I assume that I can transfer the Taylor's "frozen field" hypothesis to a fixed phase of the flow and consider that phase a quasi-steady. I am not sure if the distribution of the turbulent scales is homogeneous though. Regarding the third dimension, right now I have only 2D data experimental (U,V) in two perpendicular planes. I wanted to obtain turbulent characteristic of that data before attempting to replicate it with 3D CFD. Do you think my approach is correct for those goals? Thanks! |
|
|
|

|
|
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
However, if you have a periodic condition along x you can simply compute the spectrum at y=y0, that is E11(Kx, y0). The peaks you see in the spectrum indicate energetic eddies at the corresponding wavenumbers (and therefore to some lenght extent). Furthermore, the inverse Fourier transform of the spectra drives you to the correlation. |
||
|
|

|
||
|
|
|
#7 |
|
New Member
Join Date: Jun 2013
Posts: 10
Rep Power: 13  |
Hi Filippo,
The data that I currently have is 2D from experiments with a grid resolution of ~0.7mm along streamwise direction. If I understand you correctly, I can calculate R(x0,r) at y0, with the separation variable r sampled on the x-direction grid and then use it to compute the spectrum at y=y0? I wander if the spatial resolution of the data is enough, I can refine it if needed though. Thank you! |
|
|
|

|
|
|
|
|
#8 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
However 0.7mm says almost nothing, it can be sufficient or not depending on the energy production. What about the Re number? Fluid is air? How you can refine the space interval? You can repeat the experiment and reduced the probe measurement? |
||
|
|

|
||
|
|
|
#9 |
|
New Member
Join Date: Jun 2013
Posts: 10
Rep Power: 13  |
Thanks Filippo!
I can potentially refine the the spatial interval by reprocessing the data with a smaller interrogation window (data is from PIV). I guess realistically, the refinement will not be significant. The fluids is liquid and Re is not fixed since the flow is pulsatile. I would like to try your suggestion and compute energy spectrum of V(x, y0), the only method I knew was to take FFT of 2pt velocity correlation. Is there an alternative way of doing this? |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
it is simple using the FFT, take your velocity vector v(1:M,y0) and compute the Fourier coefficients C(Kx,y0), then compute the modulus of the coefficients and plot along Kx. Use a logarithmic scale for clarity
 Just as example, here are few lines I use in Matlab for the streamwise spectrum at some fixed Yj value % 1) ____________ Calcolo di E_uu (stream-wise)______________ % ff è un vettore di appoggio su cui fare la FFT for i = 1:np+1, ff(i) = u(i,j,k); end % Trasformata discreta calcolo dei coefficienti di Fourier c=fft(ff,np); for q = 1:np, c(q)=c(q)/np; end % Calcolo modulo quadro. Ciclo su ogni armonica k for q=1:np, cu(q,k)=c(q)*conj(c(q)); end |
|
|
|

|
|
|
|
|
#11 |
|
New Member
Join Date: Jun 2013
Posts: 10
Rep Power: 13  |
Thank you very much Filippo! I'll give it a try.
|
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
good, let me see some plots

|
|
|
|

|
|
|
|
|
#13 |
|
New Member
Join Date: Jun 2013
Posts: 10
Rep Power: 13  |
Here is what I got
 I am not quite sure I believe it though  I expected the energy to start a bit higher. That is something for me to think about I expected the energy to start a bit higher. That is something for me to think about  Thanks for all your help Filippo! |
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
well, consider that this is the only snapshot (I think related to some time measurement), in general the spectrum is statistically averaged. As you are studyng a pulsatile flow this average should be performed over several samples.
What is somehow strange is that the energy cascade seems to not finish... I supposed to see the dissipative part of spectrum. It seems that your resolution is poor to capture the whole spectrum.... |
|
|
|

|
|
|
|
|
#15 |
|
New Member
Join Date: Jun 2013
Posts: 10
Rep Power: 13  |
Yeah, the spatial resolution of the data was something I was worried about at the first place. While I can improve on the resolution to some extend, I don't think the improvement will be that significant.
Regarding the proper averaging you are right, the plot here was made just for one realization of the set that represent this particular time. On a related note, when starting from streamwise velocity instead of the correlation of the fluctuation part of the velocity, what normalization is applied to properly scale E and R? Can you still say that for r->0, R->1 after scaling with Urms for instance? |
|
|
|

|
|
|
|
|
#16 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
Have you fixed y0 at the center of the pipe? Concerning the scaling, the coefficient of correlation will be 1 for r=0. How do you compute the velocity fluctuation? |
||
|
|

|
||
|
|
|
#17 |
|
New Member
Join Date: Jun 2013
Posts: 10
Rep Power: 13  |
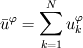 is my mean, here is my mean, here 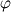 is the phase of the flow, I typically use about N=250 realizations of each phase. is the phase of the flow, I typically use about N=250 realizations of each phase.I calculate fluctuation component by subtracting mean from the instantaneous velocity. So, in this case, 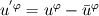 . Yes, y = y0 - middle of the pipe, was fixed. . Yes, y = y0 - middle of the pipe, was fixed.I took ifft of E, which plot is here, and while the obtained shape seems to be OK, at r=0 R is around 0.02 so I started to wander if it needs to be scaled. I'll try to refine the data and see if that will bring any improvement in the E distribution. |
|
|
|

|
|
|
|
|
#18 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
of course you have (1/N) in the mean... the ifft of E produce the correlation, hence you have to scale if you want the coefficients. But I don't think that scaling is something that can add more indication... It appears from your spectrum that you have an energy cascade without noticeable peaks... |
|
|
|

|
|
|
|
|
#19 | |
|
Senior Member
Huang Xianbei
Join Date: Sep 2013
Location: Yangzhou,China
Posts: 302
Rep Power: 14  |
Quote:
I got stuck in the post-process again and need your help. I'm calculating the two-point correlation in the channel flow DNS. As you say, if the direction is homogenous, any choice of the x will get the same result, so I only need to calculate it with a chosen x, right? I calculate it by choosing x=0 and average with 300 samples, but the curve is not smooth at all! The deltaT=0.0065h/ut, everything is in good agreement with Moin's data but this one. |
||
|
|

|
||
|
|
|
#20 | |
|
Senior Member
Huang Xianbei
Join Date: Sep 2013
Location: Yangzhou,China
Posts: 302
Rep Power: 14  |
Quote:
1.range the data to make it looks: x value in one column is the same; 2.chose x=0, so Ruu(r)=u*u(r); 3.average Ruu in z direction(spanwise,homogenous),that is, do average in each column 4.repeat with all samples 5.average |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Get Pressure and Velocity at point | Vitaly | FLUENT | 12 | January 26, 2020 23:06 |
| velocity in a specific point in cfx results | ja.maldonado1187 | CFX | 1 | February 13, 2013 20:58 |
| WSS and normal velocity gradient for the slanted pipe | wanna88 | FLUENT | 2 | October 1, 2012 23:34 |
| calculation of spatial correlation from .vtk files | vishwa | OpenFOAM | 0 | July 17, 2010 15:01 |
| Inlet Velocity in CFX | aeroman | CFX | 12 | August 6, 2009 19:42 |