 |
|
|
[Sponsors] | |||||
Time step independence study for transient CFD simulation |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#21 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
the local truncation error has terms that depend on the time and space step sizes, when you fix the h size you have as a consequence that the spatial contribution is constant. When you reduce the time step, the constant spatial error must be small, otherwise that error will hide the scaling of the temporal error
|
|
|
|

|
|
|
|
|
#22 | |
|
Member
Join Date: Sep 2018
Posts: 53
Rep Power: 8  |
Quote:
|
||
|
|

|
||
|
|
|
#23 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
In any run, you have the same constant error in space. If it is greater than the magnitude of the error in time, you will see only the constant slope. For this reason you need to get this constant error very small. |
||
|
|

|
||
|
|
|
#24 | |
|
Member
Join Date: Sep 2018
Posts: 53
Rep Power: 8  |
Quote:
"In any run, you have the same constant error in space." Agreed. "If it is greater than the magnitude of the error in time, you will see only the constant slope." Are you referring to the constant slope of the error when plotted vs. the time step? If you are, then what else do we need? Our goal in conducting a temporal sensitivity test is to determine at which time step the temporal errors are smaller than a certain tolerance. Can't we determine this time step even if the spatial errors are large? Say we halve the time step and our solution changes by 0.01%, isn't that an indicator that our time step is adequate for the problem? |
||
|
|

|
||
|
|
|
#25 | |
|
Senior Member
Join Date: Jun 2011
Posts: 208
Rep Power: 16  |
Quote:
I also knew about calculating the step from the courant number and the mesh size but the resultant step value was usually so low that it would've taken months to simulate. |
||
|
|

|
||
|
|
|
#26 | |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,763
Rep Power: 66    |
Quote:
In order to observe the order of convergence, you need to be able to see the error decrease with smaller time-step size. If the error isn't changing, then you wont be able to see the order of convergence (regardless of whether your absolute error is very large or very small). If the temporal error is hiding beneath a large (possibly even constant) spatial error, it can be very very difficult to realize this. |
||
|
|

|
||
|
|
|
#27 | |
|
Member
Join Date: Sep 2018
Posts: 53
Rep Power: 8  |
Quote:
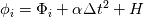 , where , where 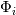 is the exact solution, is the exact solution, 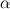 is a constant that is independent of time step and is a constant that is independent of time step and 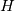 represents higher order terms that are negligible when the time step is reduced below a certain threshold. But when the spatial errors are large enough, they can magnify these higher order terms so that they are not negligible, messing up our temporal sensitivity analysis. Is this correct? represents higher order terms that are negligible when the time step is reduced below a certain threshold. But when the spatial errors are large enough, they can magnify these higher order terms so that they are not negligible, messing up our temporal sensitivity analysis. Is this correct? If it is, might it be possible that we could run a successful temporal sensitivity study even if the spatial errors aren't an order of magnitude lower than the temporal errors? I say this because those higher order terms might still be negligible if our time step is small enough and our spatial error isn't too large. Obviously, our analysis would be much more rigorous if the spatial error was negligible in comparison to the temporal error, like Filippo said, but I've run a temporal error analysis on a not very fine mesh and and have obtained a nice linear plot for the temporal error. I used first order temporal discretization and obtained a slope of close to 1. Thank you both. |
||
|
|

|
||
|
|
|
#28 |
|
Senior Member
|
I have attached an image from a very old report of one of my university classes, where I did a temporal accuracy analysis with fixed grid size.
This is what happens when you refine the time step without properly refining the grid. At a certain point, unless you refine the grid properly, for sufficiently small time steps, you will hit the spatial accuracy barrier. Hopefully, this is more clear. |
|
|
|

|
|
|
|
|
#29 | |
|
Member
Join Date: Sep 2018
Posts: 53
Rep Power: 8  |
Quote:
|
||
|
|

|
||
|
|
|
#30 |
|
Senior Member
|
The reason this happens is that the error behaves like:
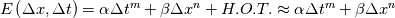 So, first of all (as it seems to be a point of confusion), higher order terms have no role in what you see here and can be discarded completely. What happens when you reduce the time step but not the grid step is that, at some point, when 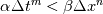 the error E will increasingly be more and more dominated by the spatial error, which is kept constant. At some point you have the error E will increasingly be more and more dominated by the spatial error, which is kept constant. At some point you have 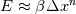 because the temporal error is negligibly small with respect to the spatial one. because the temporal error is negligibly small with respect to the spatial one.To be more specific, imagine that you have: 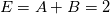 with A = 1 and B = 1. Then you start reducing B with fixed A. Then what happens is, at most, when B = 0, E = A = 1 and will not reduce any more. More formally: 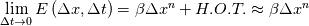 If you think about it, it is really that simple as understanding the previous limit EDIT: H.O.T. terms are negligible because if the steps are sufficiently smaller than 1, their higher order powers are negligible with respect to the lowest order ones (m and n here) |
|
|
|

|
|
|
|
|
#31 |
|
Senior Member
|
What happens at large steps is completely case dependent, so never expect anything there. What if my exact solution has any of the higher order derivatives expected in H.O.T. as exactly 0?
|
|
|
|

|
|
|
|
|
#32 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
I try to be more rigorous.
The local truncation error defines the accuracy order of the scheme. I suppose you are evaluating the discretization error from a known and available exact solution. They are related but not equal, thus you need to assess if evaluating the discretization error you are able to deduce correctly the accuracy order defined by the lte. Now, by defining the discretization error as the ed =(fex-fn), you have to consider both the original PDE satisfied by fex A fex=0 and the discrete equation satisfied by fn Ad fn =0 . The lte is defined as (A-Ad) fex = lte and Ad (fex-fn) = -lte thus ed = Ad^-1 (-lte) Therefore, your goal is to evaluate lte for assessing the accuracy order but you practically compute ed. If you fix the grid size, a part of the lte will be constant while the remaining part will tend to zero for dt going to zero. As a consequence, the discretization error will be constant at a certain value as Paolo shown. I suggest to read section 8.2 in the textbook of Leveque about FV methods. |
|
|
|

|
|
|
|
|
#33 |
|
Member
Join Date: Sep 2018
Posts: 53
Rep Power: 8  |
Ah, I see where I was going wrong now. On page 59 of Ferziger, the discretization error is expanded as
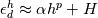 . . The exact solution is then given as 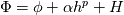 . .Though I don't think he explicitly mentions it, this must be for a time independent system of equations, as the Taylor expansion is about zero. I mistakenly assumed that for constant spatial discretization error, I could expand the temporal discretization error as 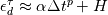 and then write the exact solution as and then write the exact solution as 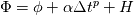 , where , where 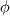 is the discretized solution. This equation says that as the time step becomes smaller, the discretized solution converges to the exact solution, which is obviously not what happens, unless the spatial discretization error is also zero. is the discretized solution. This equation says that as the time step becomes smaller, the discretized solution converges to the exact solution, which is obviously not what happens, unless the spatial discretization error is also zero. But I have another question, if the error for a time dependent system of equations is, as you wrote, 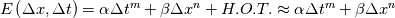 Then the exact solution is 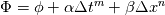 Now, if we calculate the error as 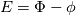 , and successively reduce the time step, then, like you and Filippo said, after a certain point the spatial error will dominate and reductions in the time step will yield almost no change in the calculated error. But what if we calculate the error as the difference between each solution and a solution with a very small time step ( , and successively reduce the time step, then, like you and Filippo said, after a certain point the spatial error will dominate and reductions in the time step will yield almost no change in the calculated error. But what if we calculate the error as the difference between each solution and a solution with a very small time step (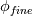 )? For a very small time step )? For a very small time step 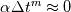 and the exact solution would be given by and the exact solution would be given by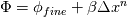 Then if we calculate the error as 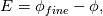 we get 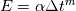 , , which reveals the order of the temporal error, m, regardless of how large the spatial discretization error is. The only issue I see with this approach is that if the spatial error is too large, limited machine precision could prevent us from seeing the small changes in the solution. What do you guys think? |
|
|
|

|
|
|
|
|
#34 |
|
Member
Join Date: Sep 2018
Posts: 53
Rep Power: 8  |
Yeah I'm reading Leveque's book right now. There's a very nice discussion about error norms there, but I can't find an answer to another question that's been bugging me. If our discretization method is second order accurate in space and time, is it reasonable to expect that time and spatial integrations of solution variables will also be second order accurate? For example, if the fluid velocity is second order accurate in space and time, is the average flow rate over a period of time also second order accurate? My own analysis with Taylor series indicates that it is.
|
|
|
|

|
|
|
|
|
#35 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
Why not? The flow rate is only an integral quantity computed from your second order accurate velocity, you need only to take care in computing it at second order of accuracy and compare to the exact flow rate. |
||
|
|

|
||
|
|
|
#36 |
|
Senior Member
|
Quote:
Yet, things are more complicate than this. You actually need a time step that while making the time error small, will still advance your solution in a meaningful way without hitting precision issues. Also, you are underestimating the effort to advance such a solution in time: 1 s at dt = 1e-9 s indeed requires 1e9 time steps. Also, I haven't done the math, but I'm pretty sure that non-linearity is not gonna help in this experiment. Nor I'm sure this is going to work with any scheme. But you can certainly make an experiment with a simple 1d case. |
|
|
|

|
|
|
|
|
#37 | |
|
Senior Member
Join Date: Jun 2011
Posts: 208
Rep Power: 16  |
Quote:
If I select a step that is say 1e6 larger, then the simulation would obviously run much faster. This however totally violates the courant number<0.7 rule. If during the simulation the convergence at each step looks OK, then would the final result still be trustful? |
||
|
|

|
||
|
|
|
#38 | |
|
Senior Member
|
Quote:
You see how, the initial dt0 is kind of arbitrary. But the smaller it is, the less you eventually see in your study. Let's say dt0 = 0.1, so you need to evaluate the solution at T = 0.4 s. But you can also just say dt0 = 1e-7s and end up with just 400 time steps for dt=1e-9s. I would, honestly, not suggest to run this on a case that takes 10 min to complete a single time step. As you suggest, there are Courant issues to consider in all of this as well. But if you want to make this experiment (as opposed to one where both dx and dt vary) you still need to set up a grid that works at dt0. That one basically defines your path. The coarsest it is, the faster you will be. But, honestly, we are talking of an experiment where you have the analytical solution, I don't see how the coarsest grid could be so heavy to require 10 min for a single step. This mostly academic experiment demands cases with a single time step cost in the order of seconds, not more. |
||
|
|

|
||
|
|
|
#39 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,763
Rep Power: 66    |
||
|
|

|
|
|
|
|
#40 |
|
Senior Member
|
Let me restate things more formally. The numerical solution can be written as:
![\phi_n\left( \Delta x, \Delta t \right) = \phi_e + \alpha \Delta t^m + \beta \Delta x^n + \left[ r_x \left( \Delta x \right) + r_t \left( \Delta t \right) \right] \phi_n\left( \Delta x, \Delta t \right) = \phi_e + \alpha \Delta t^m + \beta \Delta x^n + \left[ r_x \left( \Delta x \right) + r_t \left( \Delta t \right) \right]](/Forums/vbLatex/img/16b4e2fcc43aa2c87baf0d6dddd84f00-1.gif) where the terms in square parentheses are the H.O.T. in space and time respectively. We can then write the error like: ![e \left(\Delta x, \Delta t\right) = \phi_n - \phi_e = \alpha \Delta t^m + \beta \Delta x^n + \left[ r_x \left( \Delta x \right) + r_t \left( \Delta t \right) \right] = e_x + e_t e \left(\Delta x, \Delta t\right) = \phi_n - \phi_e = \alpha \Delta t^m + \beta \Delta x^n + \left[ r_x \left( \Delta x \right) + r_t \left( \Delta t \right) \right] = e_x + e_t](/Forums/vbLatex/img/b5ba996a12f5748e8062c59137d2b112-1.gif) Now, if you can compute a numerical solution with vanishing dt, you have: ![\phi_n\left( \Delta x, 0 \right) = \phi_e + \beta \Delta x^n + \left[ r_x \left( \Delta x \right) \right] \phi_n\left( \Delta x, 0 \right) = \phi_e + \beta \Delta x^n + \left[ r_x \left( \Delta x \right) \right]](/Forums/vbLatex/img/7d62556422c1c735c49d0450656036b7-1.gif) Then it follows that: ![\phi_n\left( \Delta x, \Delta t \right) - \phi_n\left( \Delta x, 0 \right) = \alpha \Delta t^m + \left[r_t \left( \Delta t \right) \right] = e_t \phi_n\left( \Delta x, \Delta t \right) - \phi_n\left( \Delta x, 0 \right) = \alpha \Delta t^m + \left[r_t \left( \Delta t \right) \right] = e_t](/Forums/vbLatex/img/9ac0d57349d5f9b02fff3c9af4a399d3-1.gif) Note that this is, sort of, what you do when you want to estimate the error without having an exact solution. EDIT: I was referring to my previous post, which was without any math, not the Lucky Tran one which is indeed correct. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Superlinear speedup in OpenFOAM 13 | msrinath80 | OpenFOAM Running, Solving & CFD | 18 | March 3, 2015 06:36 |
| directMapped problem | panda60 | OpenFOAM Bugs | 4 | July 8, 2010 11:23 |
| Time step in transient simulation | shib | FLUENT | 0 | June 17, 2010 14:07 |
| calculation diverge after continue to run | zhajingjing | OpenFOAM | 0 | April 28, 2010 05:35 |
| IcoFoam parallel woes | msrinath80 | OpenFOAM Running, Solving & CFD | 9 | July 22, 2007 03:58 |