 |
|
|
[Sponsors] | |||||
How to solve an eigenvalue problem with a constant? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: Apr 2013
Posts: 15
Rep Power: 13  |
||
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Maybe I do not understand well your question ...but if you have an eigenvalue \lambda and q is an eigenvector, then it is required that the vector a is parallel to q, right?
|
|
|
|

|
|
|
|
|
#3 | |
|
New Member
Join Date: Apr 2013
Posts: 15
Rep Power: 13  |
Quote:
Thank you. I start to understand what you mean by a should be parallel to q. BUt in general, a could make any angle w.r.t q. Since q is unknown for the moment, we don't know what's the angle a makes with q... Shu Last edited by shubiaohewan; April 6, 2013 at 12:47. |
||
|
|

|
||
|
|
|
#4 |
|
New Member
Join Date: Mar 2013
Posts: 1
Rep Power: 0  |
||
|
|

|
|
|
|
|
#5 | |
|
New Member
Gerrit Laube
Join Date: Feb 2013
Posts: 5
Rep Power: 13  |
Quote:
 and "+ 1" is and "+ 1" is 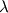 ) while you will only find n unknowns (e.g. ) while you will only find n unknowns (e.g.  ) by solving the linear system. In other words, there is one ) by solving the linear system. In other words, there is one  for every for every 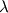 you can think of. you can think of. Anyway, there are n 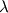 for which you will not only find one but infinitely many solutions. These are the Eigenvalues and these are the same as in for which you will not only find one but infinitely many solutions. These are the Eigenvalues and these are the same as in  because Eigenvalue only means "the value of because Eigenvalue only means "the value of 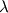 that makes that makes 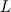 linearly dependent". You will find a linearly dependent matrix by setting its determinant to 0, which is the "characteristic equation" you might have heard of. In that case, an Eigenvector is one of these infinitely many solutions (e.g. if the Eigenvector for a 2x2 matrix is [1;2] it could also be [2;4] and so on). linearly dependent". You will find a linearly dependent matrix by setting its determinant to 0, which is the "characteristic equation" you might have heard of. In that case, an Eigenvector is one of these infinitely many solutions (e.g. if the Eigenvector for a 2x2 matrix is [1;2] it could also be [2;4] and so on).Back to your question: You could find some kind of Eigenvector and Eigenvalue, which is the same as in the original Eigenvalueproblem and additionally you will find infinitely many other solutions for infinitely many other 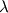 . In the real Eigenvalueproblem, these infinitely many solutions are all 0, which is why you search for the only non-zero solution. But in your case most of them will be non-zero solutions and only you are able to know what this might mean. . In the real Eigenvalueproblem, these infinitely many solutions are all 0, which is why you search for the only non-zero solution. But in your case most of them will be non-zero solutions and only you are able to know what this might mean.My hones advice: You should check if this equation is really what you want/need to solve! Good Luck! |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| how to solve large scale problem | send1000 | ANSYS | 0 | September 3, 2011 14:46 |
| how to solve a problem involving both laminar and turbulent flow | seefd | FLUENT | 1 | June 3, 2011 04:20 |
| CGNS lib and Fortran compiler | manaliac | Main CFD Forum | 2 | November 29, 2010 07:25 |
| Can FLUENT solve this type of problem? | Whitaker | FLUENT | 3 | October 23, 2000 04:01 |
| use of MAC method to solve sloshing problem. | S.R.SAHI | Main CFD Forum | 1 | April 15, 1999 23:28 |