 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Join Date: Jun 2010
Posts: 111
Rep Power: 16  |
Can anyone suggest a good paper or book on the use of finite volume methods for solids?
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Rami Ben-Zvi
Join Date: Mar 2009
Posts: 155
Rep Power: 17  |
||
|
|

|
|
|
|
|
#3 |
|
New Member
RZA
Join Date: Nov 2012
Posts: 25
Rep Power: 13  |
Hi
I think FVM is preferably right choice to analyze solid structures. Most of the FVM literature is available in the perspective of computational fluid dynamics. So you should consult CFD books. 1. Computational Fluid Dynamics: Principles & Applications By J. Blazek 2. Computational Fluid Dynamics By Hoffman |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Join Date: Jun 2010
Posts: 111
Rep Power: 16  |
I am interested in the governing equations and their discretizations for stress analysis problems. I'm familiar with fvm for fluids, solid equation are somewhat different. In particular I am interested in the stress term ...
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Rami Ben-Zvi
Join Date: Mar 2009
Posts: 155
Rep Power: 17  |
Hi Hooman,
The equations used in stress analysis for solids are nearly identical to those of the momentum equations for viscous fluid flow, except that for solids 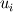 stands for the displacement vector, whereas for fluids - it is the velocity (the stress is related to strain for solid and to strain-rate in fluids). stands for the displacement vector, whereas for fluids - it is the velocity (the stress is related to strain for solid and to strain-rate in fluids).You should also choose whether you use an Eulerian or Lagrangian formulation. The Lagrangian formulation in Cartesian coordinates is simply  (using tensor notation where D/Dt is the material derivative, comma is the covariant derivative - which degenerates to simple spatial derivative in Cartesian coordinates, (using tensor notation where D/Dt is the material derivative, comma is the covariant derivative - which degenerates to simple spatial derivative in Cartesian coordinates, 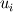 is the displacement, is the displacement,  is the stress, is the stress,  is the body force and is the body force and 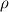 is the density). is the density).If you treat small displacement and small strain, the various stress and strain measures (Cauchy, Piola-Kirchhoff, Green, Lagrange, etc.) are identical and their relation to each other are practically the same as those for fluids, e.g. for elasticity  , where , where 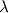 and and 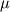 are the Lame modulii and are the Lame modulii and  . .Nevertheless, I still suggest to look into FEM, which has much more literature on solids. It is in many ways similar (and more consistent and general) to FVM. Actually, FVM can be viewed as a special case of FEM, using piecewise-constant shape-functions and some additional minor approximations. Last edited by Rami; December 5, 2012 at 07:20. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Usage of fvm and fvc | dl6tud | OpenFOAM Programming & Development | 1 | July 27, 2012 19:28 |
| FVM in 1-D spherical coordinates | lost.identity | Main CFD Forum | 0 | January 17, 2011 10:06 |
| FVM vs FEM | elwolv | Main CFD Forum | 8 | June 5, 2007 14:23 |
| comments on FDM, FEM, FVM, SM, SEM, DSEM, BEM | kenn | Main CFD Forum | 2 | July 18, 2004 19:28 |
| References for FVM | Anthony Wachs | Main CFD Forum | 8 | February 20, 2002 20:23 |