 |
|
|
[Sponsors] | |||||
|
|
|
#21 | |
|
Member
misagh
Join Date: Apr 2012
Posts: 64
Rep Power: 14  |
Quote:
How are you sure about the experimental results, since experimental investigations have some error. The fact that your numerical results do not exactly fit with the expwrimental results can be due to poor mesh quality or bad boundary condition or use of inappropriate models in the solver. |
||
|
|

|
||
|
|
|
#22 |
|
Senior Member
A. Min
Join Date: Mar 2015
Posts: 308
Rep Power: 12  |
Hi all,
I have read many papers in which use two different formulas for Viscous Dissipation: tau : grad(U) tau : D where D = 0.5* ( grad(U) + transpose(grad(U)) ) Which one is correct? Basically, Is there any difference between Stress Work & Viscous Dissipation? Thanks |
|
|
|

|
|
|
|
|
#23 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
the correct definition is mu*S:S wherein S is the simmetric velocity gradient |
||
|
|

|
||
|
|
|
#24 |
|
Senior Member
A. Min
Join Date: Mar 2015
Posts: 308
Rep Power: 12  |
||
|
|

|
|
|
|
|
#25 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
||
|
|

|
|
|
|
|
#26 |
|
Senior Member
A. Min
Join Date: Mar 2015
Posts: 308
Rep Power: 12  |
||
|
|

|
|
|
|
|
#27 | ||
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,762
Rep Power: 66    |
Quote:
The stress work in the energy equation is:  and this can be expanded to: 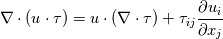 The dissipation function is only the last part  The other term corresponds to a reversible transfer of kinetic/potential energy of the flow following the work-energy theorem (you can think of it as u times the momentum equation). An example of this effect is in a developing pipe flow with uniform velocity inlet, and this is most easily seen in the laminar case. The effect of viscous forces accelerates the flow in the center of the pipe to higher than the inlet (into a parabolic profile). If stress work was purely dissipative, the flow wouldn't accelerate. Only the last term corresponds to the irreversible conversion into thermal energy. Here it is not shown how the last term is irreversible. To do this proof, you have to show that it is positive semi-definite (and maybe invoke some thermodynamic arguments). Physics aside, that leads back to your actual question... Quote:
However, D is computationally efficient because it is a symmetric tensor (less memory and faster to operate on). In numerical codes, it would make sense to use always compute  instead of instead of 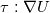 . Tau can be arbitrary without loss of generality so it works for newtonian and non-newtonian fluids. . Tau can be arbitrary without loss of generality so it works for newtonian and non-newtonian fluids.
|
|||
|
|

|
|||
|
|
|
#28 |
|
Senior Member
A. Min
Join Date: Mar 2015
Posts: 308
Rep Power: 12  |
Quote:
It seems that is what I want. However, I have 2 other questions: 1. why do some papers use viscous diss = tau : D instead of what you mentioned (tau:gradU)? 2. what is exactly the first term? when is it important ? why didn't usually we see it in fluid mechanics papers? regards, Ali |
|
|
|

|
|
|
|
|
#29 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
The relation you are referring to is tau = mu(strain)*S. The relation is similar to that of Newtonian fluid but is non linear in the viscosity. The definition of the viscous dissipation (a term you will find in the balance of kinetic energy and, with changed sign, in the balance of internal energy) is straightforward. |
||
|
|

|
||
|
|
|
#30 | |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,762
Rep Power: 66    |
Quote:
2. First, you find it in the energy equation. Fluid mechanics papers which only write down the continuity and momentum equations (i.e. the Navier-Stokes equations) will never show you this dissipation term (since dissipation is energy and not momentum). Second, the first term exactly balances the kinetic energy and potential energy so you can easily do some manipulations on your energy equation and it cancels some other terms. Depending on which form of energy equation you write down (and there are dozens of equally valid forms all in popular usage), you may or may not see the term. |
||
|
|

|
||
|
|
|
#31 |
|
Senior Member
A. Min
Join Date: Mar 2015
Posts: 308
Rep Power: 12  |
Quote:
That was really helpful. Thanks for participation in this discussion. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| calculating the viscous stress tensor tau for viscous dissipation heating | dgadensg | OpenFOAM Programming & Development | 5 | January 17, 2023 16:20 |
| viscous dissipation modelling | mahjoob | FLUENT | 0 | January 31, 2007 19:52 |
| temperature rise due to viscous dissipation | Marek | Main CFD Forum | 6 | December 30, 2004 17:24 |
| VISCOUS heat dissipation | Joseph | CFX | 0 | October 1, 2004 09:52 |
| Is the viscous dissipation term fully included? | yann | Phoenics | 0 | June 5, 2003 11:23 |