 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 16  |
Dear CFD-onliners,
I came across a question when trying to solve the momentum equation following Patankar's book (1980) indications. When solving a general transport equation for a certain variable 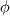 , the discretized form takes the form: , the discretized form takes the form: , where P,E,W,N,S stand for point, east face, west face, north face and south face, respectively. The coefficients depend on the type of numerical scheme used (central differences, upwind, exponential, power law...). My question: how do we calculate the discretization coefficients for the momentum equations u and v? can we just assume that the momentum equations are another set of convection-diffusion equations, where the variable 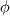 are u and v? Then we could just use the same method as before (upwind, power law, ...). are u and v? Then we could just use the same method as before (upwind, power law, ...).Any help will be welcome. Thanks in advance  . .
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Chris DeGroot
Join Date: Nov 2011
Location: Canada
Posts: 414
Rep Power: 18  |
Quote:
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Join Date: Dec 2011
Location: Madrid, Spain
Posts: 134
Rep Power: 16  |
Hi Chris, I found later in Patankar's book that we could just use any differentiation scheme for the diffusive and convective terms in the momentum equation, as it is done for general convection-diffusion equations (I also found the coefficients I was looking for in Versteeg&Malalasekera book).
Yes, I will treat the pressure gradient term differently don't worry. I appreciate your reply anyway. Cheers. |
|
|
|

|
|
|
|
|
#4 | |
|
Senior Member
Join Date: Aug 2011
Posts: 272
Rep Power: 16  |
Quote:
The momentum equations are EXACTLY convection-diffusion equations with a source term. In this case the source term is the pressure gradient (dp/dx_i) + cross derivative of velocity (du_j/dx_i). (here d is partial derivative) It can be discretized using the same schemes as the ones used for any scalar transport equation. The scalars here are the componnents of the velocity vector u and v. |
||
|
|

|
||
|
|
|
#5 | |
|
Senior Member
Chris DeGroot
Join Date: Nov 2011
Location: Canada
Posts: 414
Rep Power: 18  |
Quote:
|
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| solving the momentum equation in UEqn. | callahance | OpenFOAM | 2 | October 18, 2012 10:38 |
| Question on the discretization of momentum equation in icoFoam | MPJ | OpenFOAM | 3 | October 4, 2011 10:44 |
| Momentum equation of Darcy's law | sambatra | OpenFOAM Running, Solving & CFD | 2 | April 17, 2009 04:27 |
| Momentum Equation | Munir Ahmed Khan | FLUENT | 0 | August 27, 2008 08:57 |
| Question on momentum equation in VOF or Level Set | Kai Yan | Main CFD Forum | 0 | January 11, 2008 09:47 |