 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Join Date: Dec 2014
Posts: 38
Rep Power: 12  |
Dear colleagues,
I would like to make sure if my approach is correct: I need to calculate equation for a source: phi *  (alpha*V) (alpha*V)alpha - void fraction phi - UDS V - velocity In the DEFINE_SOURCE I iterate over all cell's faces and on each cell (I took central differencing scheme to get values on the faces in interior): c_face_loop(c, t, i) /* I added all variables but to understand approach it is not necessary to show them all */ { F_AREA(Area,f,t); vec[0] = (C_U(c0,t0)*C_U(c1,t1))/2*(C_VOF(c0,t0)*C_VOF(c1,t1))/2; vec[1] = (C_W(c0,t0)*C_W(c1,t1))/2*(C_VOF(c0,t0)*C_VOF(c1,t1))/2; vec[2] = (C_V(c0,t0)*C_V(c1,t1))/2*(C_VOF(c0,t0)*C_VOF(c1,t1))/2; velocity += NV_DOT(vec, Area); } return velocity * C_UDSI(c,t,0); Is a good approach? I put some conditions for boundaries, but they are not important to understand the approach. But the question is should I take dot product of a vectors? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Nov 2013
Posts: 1,965
Rep Power: 27  |
||
|
|

|
|
|
|
|
#3 |
|
Member
Join Date: Dec 2014
Posts: 38
Rep Power: 12  |
Thank you very much for your reply and sugestions.
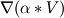 to calculate this I used face values multiplied by the area. to calculate this I used face values multiplied by the area.To get face values of alpha and velocity I used: (C_U(c0,t0)*C_U(c1,t1))/2*(C_VOF(c0,t0)*C_VOF(c1,t1))/2 - for x direction and for other direction I used other lines of the code. NV_DOT(vec, Area); - I belive this will give values of alpha * velocity * Area of a face. velocity += NV_DOT(vec, Area); - velocity variable will "store" and add all values on faces which are multiplied by the face area which should be equal the divergence. and then in return velocity * C_UDSI(c,t,0); I mulitpied C_UDSI which is phi with divergence Does it clear? I will be more than glad to try to explain what I meant if it is still not clear. Should I add whole code for DEFINE_SOURCE? |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Join Date: Nov 2013
Posts: 1,965
Rep Power: 27  |
It is not clear to me where you think you calculate the gradient. I can not find anything that corresponds to calculating a gradient, but maybe I am overlooking it.
|
|
|
|

|
|
|
|
|
#5 |
|
Member
Join Date: Dec 2014
Posts: 38
Rep Power: 12  |
I can go from divergence in the volume to the sum over all values on faces and in case of vector I need to multiply velocity values by the area normal vector. As far as I understand numerical methods Fluent uses finite volume technique, so that's way I multiply velocity times area and sum over all faces should give me a value of the surface integral of a velocity.
But I am not sure. |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Join Date: Nov 2013
Posts: 1,965
Rep Power: 27  |
But you don't have divergence, you have gradient. At least, that is what you wrote above.
|
|
|
|

|
|
|
|
|
#7 |
|
Member
Join Date: Dec 2014
Posts: 38
Rep Power: 12  |
||
|
|

|
|
|
|
|
#8 |
|
Senior Member
Join Date: Nov 2013
Posts: 1,965
Rep Power: 27  |
If you want help, you should make it easy for people to help you. You have already thought about the problem, and you took some steps to change the mathematical formulation into a computer code. Mention the steps you took, that makes it a lot easier for other people to help you.
What you did, if I guess correctly:  This is approximately equal, if phi is not changing to wildly in a cell:  And using the divergence theorem:  The first integral is simple C_UDSI(c,t,0): C_UDSI(c,t,0)  Your first post should have at least mentioned that you used the divergence theorem to simplify your equation. As you can see, I stopped somewhere in the derivation, because I can not see how you went from  to your code. Of course, I can roughly see it: I see the alpha, I see the V, and I see the area, and that you do the three dimensions separately. But why do you multiply the values for c0 and c1? Why divide by 2? What are your thoughts behind that? to your code. Of course, I can roughly see it: I see the alpha, I see the V, and I see the area, and that you do the three dimensions separately. But why do you multiply the values for c0 and c1? Why divide by 2? What are your thoughts behind that?Edit: To be clear: it is not a problem for me that you accidentally put the gradient in the equation in stead of the divergence. Those small accidents happen. And moreover, the title already mentions that your question has to do with divergence, but when I read that, I thought you meant divergence as in opposite to convergence; I thought your simulation was diverging. But is is a little bit frustrating that you ask us if your translation from mathematical equation to computer code is correct, but you don't give us the intermediate steps you take in that translation. It is easier to check ten small steps, than to check one giant jump. Mentioning that you used the divergence theorem would have made your "giant jump" a lot smaller, and easier to check. |
|
|
|

|
|
|
|
|
#9 |
|
Member
Join Date: Dec 2014
Posts: 38
Rep Power: 12  |
Sorry, I couldn't answer eariler.
First of all, thank you very much and you are right, I should be more specific from the beginning. Well,:  should be wrriten like that: should be wrriten like that:  f stands for face Fluent doesn't store values for faces because it uses differencing schemes to calculate it. In my case (C_U(c0,t0)*C_U(c1,t1))/2 ((c0, t0) and (c1,t1) are values in cells on both sides of one face - to have in mind that I iterate over all faces in one cell) will give value of a component of the  in x direction (the same with the rest) and (C_VOF(c0,t0)*C_VOF(c1,t1))/2 will give value of in x direction (the same with the rest) and (C_VOF(c0,t0)*C_VOF(c1,t1))/2 will give value of  at the face - accroding to the central differencing schemes. at the face - accroding to the central differencing schemes.Using: vec[0] = (C_U(c0,t0)+C_U(c1,t1))/2*(C_VOF(c0,t0)+C_VOF(c1,t1))/2; vec[1] = (C_W(c0,t0)+C_W(c1,t1))/2*(C_VOF(c0,t0)+C_VOF(c1,t1))/2; vec[2] = (C_V(c0,t0)+C_V(c1,t1))/2*(C_VOF(c0,t0)+C_VOF(c1,t1))/2; I will get values of velocity vector component in every direction on faces and its value is multiply by the value of  - both from central differencing scheme. - both from central differencing scheme.NV_DOT(vec, Area) - in my opinion should give  and now I need to iterate over all faces All of it is in the loop: c_face_loop(c, t, i) { } so I iterate over all faces; velocity += NV_DOT(vec, Area); - is also in the loop, so after last iteration I supposed to get:  which in my opinion is equal to which in my opinion is equal to  and in the last step in return there is a multiplication by C_UDSI Edit: There was a mistake in the first post...to be honest I don't know way (C_VOF(c0,t0)*C_VOF(c1,t1))/2; it should be (C_VOF(c0,t0)+C_VOF(c1,t1))/2, it was unprofessional, I am sorry |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Divergence of third order tensor | maka | OpenFOAM Post-Processing | 1 | July 4, 2024 15:30 |
| UDF divergence of a vector | cris | FLUENT | 3 | September 4, 2014 19:06 |
| foamCalc: Fatal io error calculating divergence of velocity field | rendagar | OpenFOAM Running, Solving & CFD | 0 | February 4, 2014 11:20 |
| How to calculate Torque for francis turbine | manish | CFX | 4 | March 15, 2007 03:57 |
| help:spectral methods & divergence free functionsn | D. Puigjaner | Main CFD Forum | 1 | August 28, 2000 11:06 |