Dark side of Amdahl's law. Epilogue
Tags mpi, parallel, scalability
Dependence of efficiency on the number of cores is a very important characteristic of scalability solver based on which one can predict the scaling limit. For simplicity we consider only one option for the solver, using the asynchronous version of the MPI exchanges Isend() + Irecv(). It is seen that the dependence of the efficiency of parallelization of the solver is linear or nearly linear, with a gradual drop in effectivity with increasing number of cores used
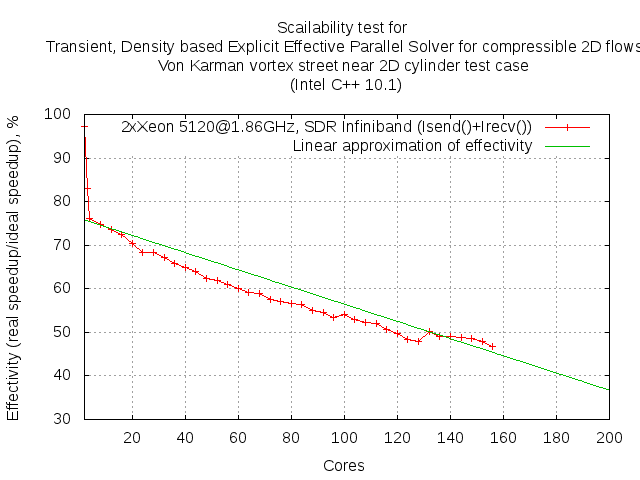 For the number of involved cores > 4 dependence of the efficiency is fairly steady linear and can be approximated by
For the number of involved cores > 4 dependence of the efficiency is fairly steady linear and can be approximated by
Thus, the speedup can be written as
Differentiating the above relation can find the approximate position of the extremum number of cores in which the speedup is terminated.
Where, n - number of involved cores.
For this particular case we have the following coefficients of the approximation
E0 = 0.762 - Parallelization efficiency for a single node (4 cores)
k = 0.0019737 - Rate of incidence of parallelization efficiency depending on the number cores.
Substituting these coefficients in the above formula (4) we find that the speedup stops when using ~193 cores
Reconstruct on the basis of (2) the dependence of speedup to the number of cores and compare it with the experimentally obtained dependence.
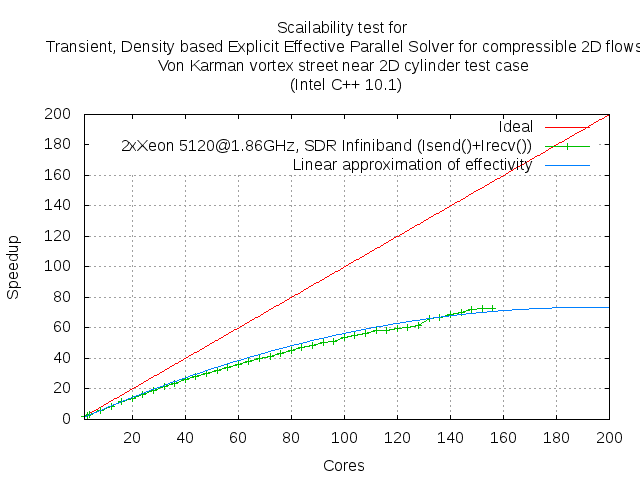 Seems to be true?
Seems to be true?
As far as universality coefficients obtained in dependence of the efficiency and how they depend on the size and nature of the current domain as well as on your hardware it will be possible only after further tests on other test cases.
This simple estimates model of scalability of solver can provide more accurately assess and allocate computing resources in case of planning a series of numerical experiments.
Code:
E(n) = E0 - k * n; (1)
Code:
Sp(n) = E(n) * n; (2)
Code:
Sp'(n) = E0 - 2 * k * n = 0; (3) n = E0 / (2 * k); (4)
For this particular case we have the following coefficients of the approximation
E0 = 0.762 - Parallelization efficiency for a single node (4 cores)
k = 0.0019737 - Rate of incidence of parallelization efficiency depending on the number cores.
Substituting these coefficients in the above formula (4) we find that the speedup stops when using ~193 cores
Reconstruct on the basis of (2) the dependence of speedup to the number of cores and compare it with the experimentally obtained dependence.
As far as universality coefficients obtained in dependence of the efficiency and how they depend on the size and nature of the current domain as well as on your hardware it will be possible only after further tests on other test cases.
This simple estimates model of scalability of solver can provide more accurately assess and allocate computing resources in case of planning a series of numerical experiments.
Total Comments 0





