Dark side of Amdahl's law. Part II
Let us consider in more detail how works domain decomposition in the simplest 1D case.
The computational domain is divided into several subdomains along one (usually the longest) dimension. The number of such subdomains usually corresponds to the number cores involved. The main data exchanges take place between neighboring subdomains. The size of transmitted data between adjacent subdomains in the general case depends on many factors (number of equations in the system, the size of the computational domain in the other dimensions of the order of the numerical scheme). However, this value does not depend on the number of subdomains on which the computational domain is divided and remains constant for a single subdomain, regardless of its size in the dimension of the partition.
Consider the unit subdomain in more detail. In the case of 1D decomposition data is exchanged between the "head" and "tail" of the neighboring subdomains (aka "Halo exchange"). The only exceptions are the first and last subdomains one of which has only the "head" and the latter only the "tail" (See Fig 1)
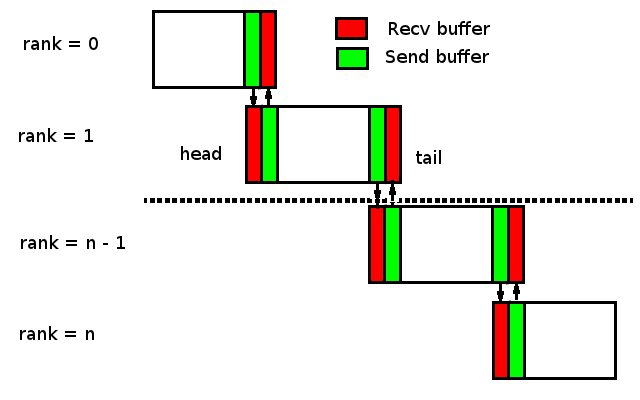
Fig. 1
To start with the easiest (and most inefficient) case by using blocking MPI calls. In this case, the solver contains code like this
The main problem with this code in the fact that at the same time can only one exchanged between neighboring subdomains. The chain of exchanges begins with the rank = n, and moves to rank = 0. The total data transfer time will depend on the number of subdomains.
Thus, the operation of data transfer it is "not parallelizable" piece of code which linked with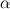 factor in Amdahl's law. Moreover, increasing the number of subdomains proportion of this part of the code increases for each subdomains. This fact is well illustrated by the experimental curves below.
factor in Amdahl's law. Moreover, increasing the number of subdomains proportion of this part of the code increases for each subdomains. This fact is well illustrated by the experimental curves below.
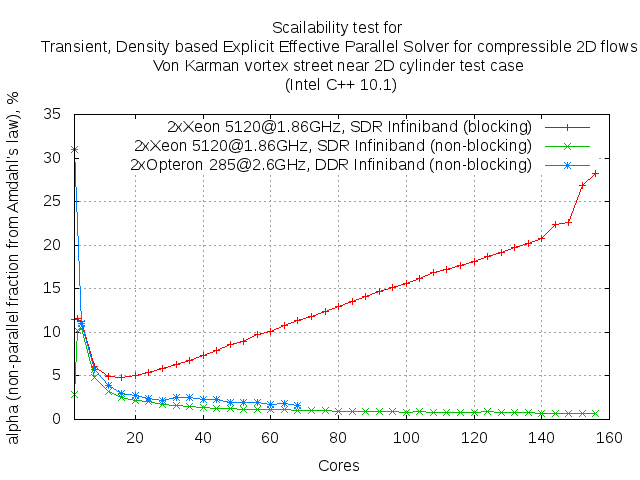
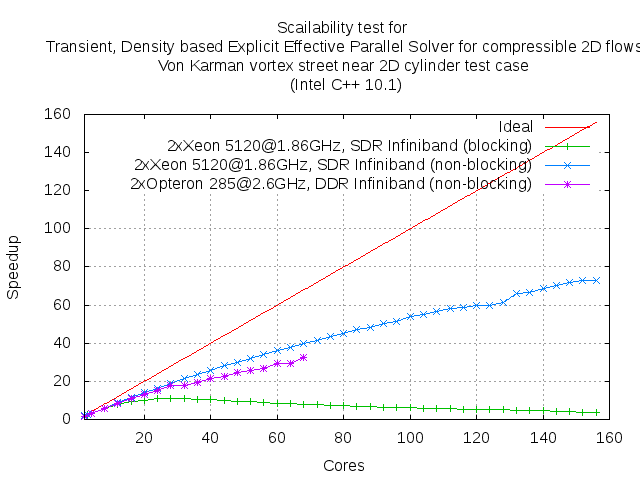
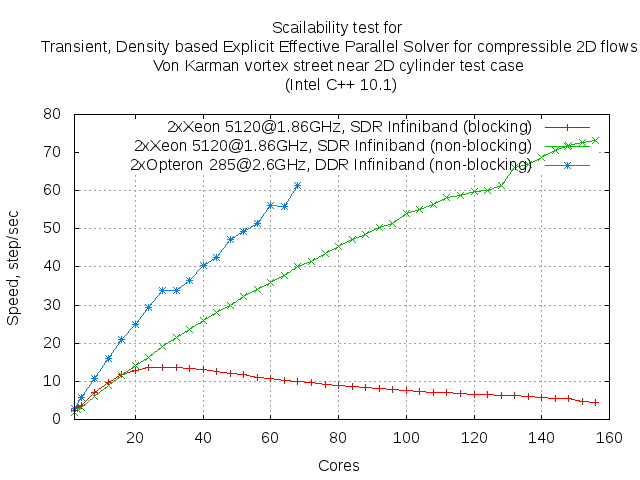
The above dependence shows that the Amdahl's law not just works and can serve as a tool for assessing the impact of such an important part of the parallel code the data exchange between subdomains
to be continued...
The computational domain is divided into several subdomains along one (usually the longest) dimension. The number of such subdomains usually corresponds to the number cores involved. The main data exchanges take place between neighboring subdomains. The size of transmitted data between adjacent subdomains in the general case depends on many factors (number of equations in the system, the size of the computational domain in the other dimensions of the order of the numerical scheme). However, this value does not depend on the number of subdomains on which the computational domain is divided and remains constant for a single subdomain, regardless of its size in the dimension of the partition.
Consider the unit subdomain in more detail. In the case of 1D decomposition data is exchanged between the "head" and "tail" of the neighboring subdomains (aka "Halo exchange"). The only exceptions are the first and last subdomains one of which has only the "head" and the latter only the "tail" (See Fig 1)
Fig. 1
Code:
// --- Halo exchange ---
if(rank < last_rank) {
// Send Tail
MPI::COMM_WORLD.Send(TailSendBuffer,
TailSize,
MPI::BYTE,
rank+1,tag_Tail);
// Recive Head
MPI::COMM_WORLD.Recv(HeadRecvBuffer,
HeadSize,
MPI::BYTE,
rank+1,tag_Head);
}
if(rank > 0) {
// Recive Tail
MPI::COMM_WORLD.Recv(RecvTailBuffer,
TailSize,
MPI::BYTE,
rank-1,tag_Tail);
//Send Head
MPI::COMM_WORLD.Send(SendHeadBuffer,
HeadSize,
MPI::BYTE,
rank-1,tag_Head);
}
Thus, the operation of data transfer it is "not parallelizable" piece of code which linked with
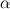 factor in Amdahl's law. Moreover, increasing the number of subdomains proportion of this part of the code increases for each subdomains. This fact is well illustrated by the experimental curves below.
factor in Amdahl's law. Moreover, increasing the number of subdomains proportion of this part of the code increases for each subdomains. This fact is well illustrated by the experimental curves below.to be continued...
Total Comments 0





