|
|||
|
Posted in LES
Views 1867
Comments 0

|
|
|||
|
Posted in LES
Views 3255
Comments 1

|
|
|||
|
Posted in Uncategorized
Views 2414
Comments 0

|
|
|||
|
Posted in Basic Fluid Mechanics and CFD
Views 1431
Comments 0

|


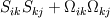
![\frac{\partial \rho}{\partial t} +
\frac{\partial}{\partial x_j}\left[ \rho u_j \right] = 0 \frac{\partial \rho}{\partial t} +
\frac{\partial}{\partial x_j}\left[ \rho u_j \right] = 0](/Forums/vbLatex/img/1194ad2165bd70d6ccac3f24ea514126-1.gif)
![\frac{\partial}{\partial t}\left( \rho u_i \right) +
\frac{\partial}{\partial x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right] = 0 \frac{\partial}{\partial t}\left( \rho u_i \right) +
\frac{\partial}{\partial x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right] = 0](/Forums/vbLatex/img/5d8b30cb9598ed5bda495dcb5ce01e1d-1.gif)

