Closing on wall functions - part 3: a standard wall function
We make the following assumption for the turbulent viscosity ratio:

where is the von Karman constant and
is the von Karman constant and  is, for the moment, an unspecified positive parameter. One can then show that the following results:
is, for the moment, an unspecified positive parameter. One can then show that the following results:
![{s_T^i}^+ =\frac{{y_{min}^+}^{i+2}}{i+2} +\frac{\left(-1\right)^{i+1}}{\left(\kappa \frac{Pr}{Pr_t}\right)^{i+2}}\left[\ln{\left(\frac{1+\kappa\frac{Pr}{Pr_t}y_{max}^+}{1+\kappa\frac{Pr}{Pr_t}y_v^+}\right)+\sum_{j=1}^{i+1} a_j \left(\frac{Pr}{Pr_t}\right)^j}\right] {s_T^i}^+ =\frac{{y_{min}^+}^{i+2}}{i+2} +\frac{\left(-1\right)^{i+1}}{\left(\kappa \frac{Pr}{Pr_t}\right)^{i+2}}\left[\ln{\left(\frac{1+\kappa\frac{Pr}{Pr_t}y_{max}^+}{1+\kappa\frac{Pr}{Pr_t}y_v^+}\right)+\sum_{j=1}^{i+1} a_j \left(\frac{Pr}{Pr_t}\right)^j}\right]](/Forums/vbLatex/img/1422f3f2c9421b063657ca4596ea1c5e-1.gif)
![{p^i}^+ =\frac{\left(-1\right)^{i+1}}{\kappa^{i+2}}\left[\left(i+2\right)\ln{\left(\frac{1+\kappa y_{max}^+}{1+\kappa y_v^+}\right)+\frac{y_v^+-y_{max}^+}{\left(1+y_v^+\right)\left(1+y_{max}^+\right)}+\sum_{j=1}^{i+1} a_j \left(i+j+2\right)}\right] {p^i}^+ =\frac{\left(-1\right)^{i+1}}{\kappa^{i+2}}\left[\left(i+2\right)\ln{\left(\frac{1+\kappa y_{max}^+}{1+\kappa y_v^+}\right)+\frac{y_v^+-y_{max}^+}{\left(1+y_v^+\right)\left(1+y_{max}^+\right)}+\sum_{j=1}^{i+1} a_j \left(i+j+2\right)}\right]](/Forums/vbLatex/img/0964bba1a61b7125f09dc78af9534689-1.gif)
where ,
,  , and:
, and:

The general problem with the standard formulation is that, while it is reasonable to pick up an value for the velocity case, even a second one for the TKE production (rigorous doesn't mean stupid, so if different
value for the velocity case, even a second one for the TKE production (rigorous doesn't mean stupid, so if different  values work better for
values work better for  and
and  , why not?), it is not reasonable to manually pick a value in
, why not?), it is not reasonable to manually pick a value in 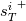 for each value of the ratio
for each value of the ratio  .
.
As it turns out, however, the above formulation requires modifying only for
only for  , but just works in all the other cases. This statement just accounts of the fact that for
, but just works in all the other cases. This statement just accounts of the fact that for  the turbulent viscosity ratio becomes less and less important, while it becomes more and more important in every detail when multiplied by the ratio
the turbulent viscosity ratio becomes less and less important, while it becomes more and more important in every detail when multiplied by the ratio  .
.
The case is correctly accounted by the present formulation because it has not neglected the 1 at the denominator of the integrand function in
case is correctly accounted by the present formulation because it has not neglected the 1 at the denominator of the integrand function in 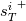 and because the solution is not arbitrarily expressed in terms of the velocity one with all the logarithmic constants lumped in a single one (typically E). The fact that the formulation still doesn't work for
and because the solution is not arbitrarily expressed in terms of the velocity one with all the logarithmic constants lumped in a single one (typically E). The fact that the formulation still doesn't work for  is just a statement of the fact that, in this case, the turbulent viscosity ratio becomes important for the temperature distribution before it does for the velocity one, so
is just a statement of the fact that, in this case, the turbulent viscosity ratio becomes important for the temperature distribution before it does for the velocity one, so  in
in 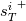 must be reduced. Let's call this new value
must be reduced. Let's call this new value  (yet, this is only needed for
(yet, this is only needed for  ).
).
As the Jayatilleke P term exactly embeds this exact same concept, it is easy to show that it can be used by computing from the following non linear, implicit equation (a similar one must be solved also for the classical standard wall function):
from the following non linear, implicit equation (a similar one must be solved also for the classical standard wall function):

where is the original value used in the velocity profile and P is the mentioned Jayatilleke term (but any similar correlation can substitute it in the equation above, say the Spalding one). I have found that, initializing
is the original value used in the velocity profile and P is the mentioned Jayatilleke term (but any similar correlation can substitute it in the equation above, say the Spalding one). I have found that, initializing  as
as  , 3 iterations of the Halley's method are sufficient to compute
, 3 iterations of the Halley's method are sufficient to compute  close to machine precision for any practical value of
close to machine precision for any practical value of  .
.

where
 is the von Karman constant and
is the von Karman constant and  is, for the moment, an unspecified positive parameter. One can then show that the following results:
is, for the moment, an unspecified positive parameter. One can then show that the following results:![{s_T^i}^+ =\frac{{y_{min}^+}^{i+2}}{i+2} +\frac{\left(-1\right)^{i+1}}{\left(\kappa \frac{Pr}{Pr_t}\right)^{i+2}}\left[\ln{\left(\frac{1+\kappa\frac{Pr}{Pr_t}y_{max}^+}{1+\kappa\frac{Pr}{Pr_t}y_v^+}\right)+\sum_{j=1}^{i+1} a_j \left(\frac{Pr}{Pr_t}\right)^j}\right] {s_T^i}^+ =\frac{{y_{min}^+}^{i+2}}{i+2} +\frac{\left(-1\right)^{i+1}}{\left(\kappa \frac{Pr}{Pr_t}\right)^{i+2}}\left[\ln{\left(\frac{1+\kappa\frac{Pr}{Pr_t}y_{max}^+}{1+\kappa\frac{Pr}{Pr_t}y_v^+}\right)+\sum_{j=1}^{i+1} a_j \left(\frac{Pr}{Pr_t}\right)^j}\right]](/Forums/vbLatex/img/1422f3f2c9421b063657ca4596ea1c5e-1.gif)
![{p^i}^+ =\frac{\left(-1\right)^{i+1}}{\kappa^{i+2}}\left[\left(i+2\right)\ln{\left(\frac{1+\kappa y_{max}^+}{1+\kappa y_v^+}\right)+\frac{y_v^+-y_{max}^+}{\left(1+y_v^+\right)\left(1+y_{max}^+\right)}+\sum_{j=1}^{i+1} a_j \left(i+j+2\right)}\right] {p^i}^+ =\frac{\left(-1\right)^{i+1}}{\kappa^{i+2}}\left[\left(i+2\right)\ln{\left(\frac{1+\kappa y_{max}^+}{1+\kappa y_v^+}\right)+\frac{y_v^+-y_{max}^+}{\left(1+y_v^+\right)\left(1+y_{max}^+\right)}+\sum_{j=1}^{i+1} a_j \left(i+j+2\right)}\right]](/Forums/vbLatex/img/0964bba1a61b7125f09dc78af9534689-1.gif)
where
 ,
,  , and:
, and:
The general problem with the standard formulation is that, while it is reasonable to pick up an
 value for the velocity case, even a second one for the TKE production (rigorous doesn't mean stupid, so if different
value for the velocity case, even a second one for the TKE production (rigorous doesn't mean stupid, so if different  values work better for
values work better for  and
and  , why not?), it is not reasonable to manually pick a value in
, why not?), it is not reasonable to manually pick a value in 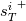 for each value of the ratio
for each value of the ratio  .
.As it turns out, however, the above formulation requires modifying
 only for
only for  , but just works in all the other cases. This statement just accounts of the fact that for
, but just works in all the other cases. This statement just accounts of the fact that for  the turbulent viscosity ratio becomes less and less important, while it becomes more and more important in every detail when multiplied by the ratio
the turbulent viscosity ratio becomes less and less important, while it becomes more and more important in every detail when multiplied by the ratio  .
.The
 case is correctly accounted by the present formulation because it has not neglected the 1 at the denominator of the integrand function in
case is correctly accounted by the present formulation because it has not neglected the 1 at the denominator of the integrand function in 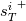 and because the solution is not arbitrarily expressed in terms of the velocity one with all the logarithmic constants lumped in a single one (typically E). The fact that the formulation still doesn't work for
and because the solution is not arbitrarily expressed in terms of the velocity one with all the logarithmic constants lumped in a single one (typically E). The fact that the formulation still doesn't work for  is just a statement of the fact that, in this case, the turbulent viscosity ratio becomes important for the temperature distribution before it does for the velocity one, so
is just a statement of the fact that, in this case, the turbulent viscosity ratio becomes important for the temperature distribution before it does for the velocity one, so  in
in 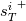 must be reduced. Let's call this new value
must be reduced. Let's call this new value  (yet, this is only needed for
(yet, this is only needed for  ).
).As the Jayatilleke P term exactly embeds this exact same concept, it is easy to show that it can be used by computing
 from the following non linear, implicit equation (a similar one must be solved also for the classical standard wall function):
from the following non linear, implicit equation (a similar one must be solved also for the classical standard wall function):
where
 is the original value used in the velocity profile and P is the mentioned Jayatilleke term (but any similar correlation can substitute it in the equation above, say the Spalding one). I have found that, initializing
is the original value used in the velocity profile and P is the mentioned Jayatilleke term (but any similar correlation can substitute it in the equation above, say the Spalding one). I have found that, initializing  as
as  , 3 iterations of the Halley's method are sufficient to compute
, 3 iterations of the Halley's method are sufficient to compute  close to machine precision for any practical value of
close to machine precision for any practical value of  .
.Total Comments 0





