A generalized thermal/dynamic wall function: Part 2
In the first part of this post we left with the problem of computing the following integral:
![f^+\left(y^+,\frac{Pr}{Pr_t}\right)=\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+} f^+\left(y^+,\frac{Pr}{Pr_t}\right)=\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}](/Forums/vbLatex/img/3cf5c7f8d4135bc15c2210e0f07028d5-1.gif)
with:

I added all the explicit functional dependencies here because we know (
( given by Monkewitz et al. and reported in the previous post), and would be great to use that solution directly. Indeed, while the above integral is still directly solvable by partial fractions (check yourself with Wolfram alpha), the solution is not really appealing, because it involves 3 non trivial roots of a cubic equation.
given by Monkewitz et al. and reported in the previous post), and would be great to use that solution directly. Indeed, while the above integral is still directly solvable by partial fractions (check yourself with Wolfram alpha), the solution is not really appealing, because it involves 3 non trivial roots of a cubic equation.
In order to avoid that, we absorb the ratio in the
in the  definition, and multiply both numerator and denumerator by
definition, and multiply both numerator and denumerator by 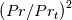 , obtaining:
, obtaining:
![\frac{\mu_t}{\mu}\left(y^+,a,k,\frac{Pr}{Pr_t}\right)=\frac{\left(\frac{Pr}{Pr_t}ky^+\right)^3}{\left(\frac{Pr}{Pr_t}ky^+\right)^2+\left[\left(ka\right)^3-\left(ka\right)^2\right]\left(\frac{Pr}{Pr_t}\right)^2} \frac{\mu_t}{\mu}\left(y^+,a,k,\frac{Pr}{Pr_t}\right)=\frac{\left(\frac{Pr}{Pr_t}ky^+\right)^3}{\left(\frac{Pr}{Pr_t}ky^+\right)^2+\left[\left(ka\right)^3-\left(ka\right)^2\right]\left(\frac{Pr}{Pr_t}\right)^2}](/Forums/vbLatex/img/20a150325f27af80998780b8f71bd610-1.gif)
Note that, if all the instances of were multiplied by
were multiplied by 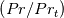 we would have done, as the trick would have been to replace
we would have done, as the trick would have been to replace  with
with  in the Monkewitz solution (that, for example, would happen for the mixing length formulation, but unfortunately it is not integrable).
in the Monkewitz solution (that, for example, would happen for the mixing length formulation, but unfortunately it is not integrable).
In order to arrive at this case, we can assume that and
and 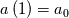 , with
, with  the value obtained by calibration with the velocity profile (11.489 for us, 10.306 for Monkewitz et al.). Then we request for
the value obtained by calibration with the velocity profile (11.489 for us, 10.306 for Monkewitz et al.). Then we request for  to be a solution of the following equation:
to be a solution of the following equation:
![\left[\left(ka_0\right)^3-\left(ka_0\right)^2\right]\left(\frac{Pr}{Pr_t}\right)^2=\left(\frac{Pr}{Pr_t}ka\right)^3-\left(\frac{Pr}{Pr_t}ka\right)^2 \left[\left(ka_0\right)^3-\left(ka_0\right)^2\right]\left(\frac{Pr}{Pr_t}\right)^2=\left(\frac{Pr}{Pr_t}ka\right)^3-\left(\frac{Pr}{Pr_t}ka\right)^2](/Forums/vbLatex/img/749983b7d74899fcf204ed64ae296919-1.gif)
It turns out that for meaningful values of and
and  the solution is:
the solution is:

with:
![\eta = \sqrt[3]{1+\theta\left(\psi+\sqrt{\psi^2+\phi}\right)} \eta = \sqrt[3]{1+\theta\left(\psi+\sqrt{\psi^2+\phi}\right)}](/Forums/vbLatex/img/f2fcd46b8600cca0cf70bb0a2e3bf6fb-1.gif)



So, with the value computed as above, we have that
value computed as above, we have that  is just the Mokewitz et al. solution given in the previous post. Thus, to complete our solution, we just need an expression for
is just the Mokewitz et al. solution given in the previous post. Thus, to complete our solution, we just need an expression for  . I won't report it here, as i just got it from Wolfram alpha (sometimes you need to add the last 3 right parentheses to the Wolfram formula, still don't know why):
. I won't report it here, as i just got it from Wolfram alpha (sometimes you need to add the last 3 right parentheses to the Wolfram formula, still don't know why):
https://www.wolframalpha.com/input/?...Batan(b%2Fc))))))
This is for the case constant. The fact that this is extendable to
constant. The fact that this is extendable to  in the form of a polynomial can be rapidly checked by integrating the separate terms multiplied by a certain power of x (i used x in place of y in Wolfram)... but i leave this as exercise for the reader
in the form of a polynomial can be rapidly checked by integrating the separate terms multiplied by a certain power of x (i used x in place of y in Wolfram)... but i leave this as exercise for the reader  .
.
In part 3 of this post (the last one) i'll sum up the steps required to compute the whole solution and give a MATLAB/Octave script that compares it with the numerical one.
![f^+\left(y^+,\frac{Pr}{Pr_t}\right)=\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+} f^+\left(y^+,\frac{Pr}{Pr_t}\right)=\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}](/Forums/vbLatex/img/3cf5c7f8d4135bc15c2210e0f07028d5-1.gif)
with:

I added all the explicit functional dependencies here because we know
 (
( given by Monkewitz et al. and reported in the previous post), and would be great to use that solution directly. Indeed, while the above integral is still directly solvable by partial fractions (check yourself with Wolfram alpha), the solution is not really appealing, because it involves 3 non trivial roots of a cubic equation.
given by Monkewitz et al. and reported in the previous post), and would be great to use that solution directly. Indeed, while the above integral is still directly solvable by partial fractions (check yourself with Wolfram alpha), the solution is not really appealing, because it involves 3 non trivial roots of a cubic equation.In order to avoid that, we absorb the ratio
 in the
in the  definition, and multiply both numerator and denumerator by
definition, and multiply both numerator and denumerator by 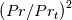 , obtaining:
, obtaining:![\frac{\mu_t}{\mu}\left(y^+,a,k,\frac{Pr}{Pr_t}\right)=\frac{\left(\frac{Pr}{Pr_t}ky^+\right)^3}{\left(\frac{Pr}{Pr_t}ky^+\right)^2+\left[\left(ka\right)^3-\left(ka\right)^2\right]\left(\frac{Pr}{Pr_t}\right)^2} \frac{\mu_t}{\mu}\left(y^+,a,k,\frac{Pr}{Pr_t}\right)=\frac{\left(\frac{Pr}{Pr_t}ky^+\right)^3}{\left(\frac{Pr}{Pr_t}ky^+\right)^2+\left[\left(ka\right)^3-\left(ka\right)^2\right]\left(\frac{Pr}{Pr_t}\right)^2}](/Forums/vbLatex/img/20a150325f27af80998780b8f71bd610-1.gif)
Note that, if all the instances of
 were multiplied by
were multiplied by 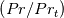 we would have done, as the trick would have been to replace
we would have done, as the trick would have been to replace  with
with  in the Monkewitz solution (that, for example, would happen for the mixing length formulation, but unfortunately it is not integrable).
in the Monkewitz solution (that, for example, would happen for the mixing length formulation, but unfortunately it is not integrable).In order to arrive at this case, we can assume that
 and
and 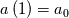 , with
, with  the value obtained by calibration with the velocity profile (11.489 for us, 10.306 for Monkewitz et al.). Then we request for
the value obtained by calibration with the velocity profile (11.489 for us, 10.306 for Monkewitz et al.). Then we request for  to be a solution of the following equation:
to be a solution of the following equation:![\left[\left(ka_0\right)^3-\left(ka_0\right)^2\right]\left(\frac{Pr}{Pr_t}\right)^2=\left(\frac{Pr}{Pr_t}ka\right)^3-\left(\frac{Pr}{Pr_t}ka\right)^2 \left[\left(ka_0\right)^3-\left(ka_0\right)^2\right]\left(\frac{Pr}{Pr_t}\right)^2=\left(\frac{Pr}{Pr_t}ka\right)^3-\left(\frac{Pr}{Pr_t}ka\right)^2](/Forums/vbLatex/img/749983b7d74899fcf204ed64ae296919-1.gif)
It turns out that for meaningful values of
 and
and  the solution is:
the solution is:
with:
![\eta = \sqrt[3]{1+\theta\left(\psi+\sqrt{\psi^2+\phi}\right)} \eta = \sqrt[3]{1+\theta\left(\psi+\sqrt{\psi^2+\phi}\right)}](/Forums/vbLatex/img/f2fcd46b8600cca0cf70bb0a2e3bf6fb-1.gif)



So, with the
 value computed as above, we have that
value computed as above, we have that  is just the Mokewitz et al. solution given in the previous post. Thus, to complete our solution, we just need an expression for
is just the Mokewitz et al. solution given in the previous post. Thus, to complete our solution, we just need an expression for  . I won't report it here, as i just got it from Wolfram alpha (sometimes you need to add the last 3 right parentheses to the Wolfram formula, still don't know why):
. I won't report it here, as i just got it from Wolfram alpha (sometimes you need to add the last 3 right parentheses to the Wolfram formula, still don't know why):https://www.wolframalpha.com/input/?...Batan(b%2Fc))))))
This is for the case
 constant. The fact that this is extendable to
constant. The fact that this is extendable to  in the form of a polynomial can be rapidly checked by integrating the separate terms multiplied by a certain power of x (i used x in place of y in Wolfram)... but i leave this as exercise for the reader
in the form of a polynomial can be rapidly checked by integrating the separate terms multiplied by a certain power of x (i used x in place of y in Wolfram)... but i leave this as exercise for the reader  .
.In part 3 of this post (the last one) i'll sum up the steps required to compute the whole solution and give a MATLAB/Octave script that compares it with the numerical one.
Total Comments 0





