Flux computation in unstructured grids
Posted July 16, 2010 at 11:49 by praveen
Tags finite volume, unstructured
Consider finite volume scheme on unstructured grids for the Euler equations.
Let be normal to a cell face and whose magnitude is equal to face area. Let
be normal to a cell face and whose magnitude is equal to face area. Let  be the conserved vector. The finite volume update equation using forward Euler time discretization is
be the conserved vector. The finite volume update equation using forward Euler time discretization is

Here is a normal vector pointing from current cell "j" into the neighbouring cell "k". Note that the conserved variable Q is updated in the global Cartesian coordinate frame.
is a normal vector pointing from current cell "j" into the neighbouring cell "k". Note that the conserved variable Q is updated in the global Cartesian coordinate frame.
As an example, the Rusanov flux would be defined as
![F(U,V,n) = \frac{1}{2}[ F(U) \cdot n + F(V) \cdot n] - \frac{1}{2} \lambda(U,V,n) (V - U) F(U,V,n) = \frac{1}{2}[ F(U) \cdot n + F(V) \cdot n] - \frac{1}{2} \lambda(U,V,n) (V - U)](/Forums/vbLatex/img/afbf757e031082087c6c22031139a5e1-1.gif)
Here, we have used the definition

where is the velocity vector, etc., and
is the velocity vector, etc., and

with being speed of sound. Note that there are many other ways to define
being speed of sound. Note that there are many other ways to define 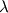 .
.
Let
 be normal to a cell face and whose magnitude is equal to face area. Let
be normal to a cell face and whose magnitude is equal to face area. Let  be the conserved vector. The finite volume update equation using forward Euler time discretization is
be the conserved vector. The finite volume update equation using forward Euler time discretization is
Here
 is a normal vector pointing from current cell "j" into the neighbouring cell "k". Note that the conserved variable Q is updated in the global Cartesian coordinate frame.
is a normal vector pointing from current cell "j" into the neighbouring cell "k". Note that the conserved variable Q is updated in the global Cartesian coordinate frame.As an example, the Rusanov flux would be defined as
![F(U,V,n) = \frac{1}{2}[ F(U) \cdot n + F(V) \cdot n] - \frac{1}{2} \lambda(U,V,n) (V - U) F(U,V,n) = \frac{1}{2}[ F(U) \cdot n + F(V) \cdot n] - \frac{1}{2} \lambda(U,V,n) (V - U)](/Forums/vbLatex/img/afbf757e031082087c6c22031139a5e1-1.gif)
Here, we have used the definition

where
 is the velocity vector, etc., and
is the velocity vector, etc., and
with
 being speed of sound. Note that there are many other ways to define
being speed of sound. Note that there are many other ways to define 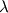 .
.Total Comments 0





