Lambda-2 criterion
The lambda 2 criterion simply concerns the definition of the scalar lambda2 and how turbulent structures can be visualized by proper isosurfaces of lambda2 (like for the Q criterion). Hence, the real difference with the scalar Q is how you compute the scalar lambda2.
This is defined as the second (in magnitude) eigenvalue of the matrix:
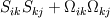
where:
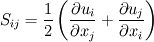
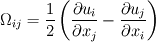
This requires the construction of the characteristic cubic equation and its resolution in order to obtain lambda2 (that is, lambda2 is the second solution of the cubic characteristic equation).
For coherent structures the matrix above can be related to the opposite of the pressure Hessian matrix. As this matrix is real and symmetric, it has two positive eigenvalues when the pressure is at minimum. As a consequence, the matrix above has two negative eigenvalues and lambda2 is certainly negative (for coherent structures). How much negative you have to pick its isosurfaces is (for what i understand) related to the visual appealing of your images (like for the Q criterion).
A basic routine for Fluent is provided below. The bug reported by the user http://www.cfd-online.com/Forums/mem...icbretzel.html has been fixed.
This is defined as the second (in magnitude) eigenvalue of the matrix:
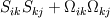
where:
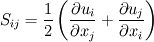
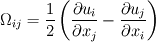
This requires the construction of the characteristic cubic equation and its resolution in order to obtain lambda2 (that is, lambda2 is the second solution of the cubic characteristic equation).
For coherent structures the matrix above can be related to the opposite of the pressure Hessian matrix. As this matrix is real and symmetric, it has two positive eigenvalues when the pressure is at minimum. As a consequence, the matrix above has two negative eigenvalues and lambda2 is certainly negative (for coherent structures). How much negative you have to pick its isosurfaces is (for what i understand) related to the visual appealing of your images (like for the Q criterion).
A basic routine for Fluent is provided below. The bug reported by the user http://www.cfd-online.com/Forums/mem...icbretzel.html has been fixed.
Total Comments 1
Comments
-
 Great addition to community. Thanks for your valuable information. Please keep it up.
Great addition to community. Thanks for your valuable information. Please keep it up.Posted July 1, 2013 at 14:33 by Far 





