Velocity-pressure coupling
From CFD-Wiki
If we consider the discretised form of the Navier-Stokes system, the form of the equations shows linear dependence of velocity on pressure and vice-versa. This inter-equation coupling is called velocity pressure coupling. A special treatment is required in order to velocity-pressure coupling. The methods such as:
- SIMPLE
- SIMPLER
- SIMPLEC
- PISO
provide an useful means of doing this for segregated solvers. However it is possible to solve the system of Navier-Stokes equations in coupled manner, taking care of inter equation coupling in a single matrix.
Contents |
Formulation
we have at each cell descretised equation in this form,
 ; Where V = Volume of cell.
; Where V = Volume of cell.
According to Rhie-Chow interpolation, we have
For continuity :
so we get:
this gives us:
defining 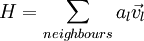
from this a pressure correction equation could be formed as:
This is a poisson equation.
Here the gradients could be used from previous iteration.
SIMPLE
See SIMPLE algorithm
SIMPLER
SIMPLEC
PISO
See PISO algorithm
Return to:


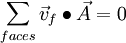
![\sum\limits_{faces} \left[ {\frac{{\sum\limits_{neighbours} {a_l } \vec v_l }}{{a_p }}} \right]_{face} - \sum\limits_{faces} \left[ {\frac{{\nabla p}}{{a_p V}}} \right]_{face} = 0](/W/images/math/6/5/1/65100ec40e98e9e08933f5de1ba3a251.png)
![\sum\limits_{faces} \left[ {\frac{{\sum\limits_{neighbours} {a_l } \vec v_l }}{{a_p }}} \right]_{face} = \sum\limits_{faces} \left[ {\frac{{\nabla p}}{{a_p V}}} \right]_{face}](/W/images/math/9/1/e/91e3d628f26bbcfa0097aa05d58e5ae5.png)
![\sum\limits_{faces} \left[ {\frac{1}{{a_p }}H} \right]_{face} = \sum\limits_{faces} \left[ {\frac{1}{{a_p }}\frac{{\nabla p}}{V}} \right]_{face}](/W/images/math/8/7/1/8716a0f2e3b6892c158df26a9c5b8c67.png)
![\sum\limits_{faces} \left[ {\frac{1}{{a_p }}H} \right]_{face} - \sum\limits_{faces} \left[ {\frac{1}{{a_p }}\frac{{\nabla p^* }}{V}} \right]_{face} = \sum\limits_{faces} \left[ {\frac{1}{{a_p }}\frac{{\nabla p^' }}{V}} \right]_{face}](/W/images/math/e/8/2/e82789c4224363527a3160a3cc2d8c1d.png)