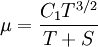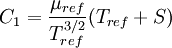Sutherland's law
From CFD-Wiki
(Difference between revisions)
m |
|||
| (2 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | In 1893 [http://en.wikipedia.org/wiki/William_Sutherland_(physicist) William Sutherland], an Australian physicist, published a relationship between the dynamic | + | In 1893 [http://en.wikipedia.org/wiki/William_Sutherland_(physicist) William Sutherland], an Australian physicist, published a relationship between the dynamic viscosity, <math>\mu</math>, and the absolute temperature, <math>T</math>, of an ideal gas. This formula, often called Sutherland's law, is based on kinetic theory of ideal gases and an idealized intermolecular-force potential. Sutherland's law is still commonly used and most often gives fairly accurate results with an error less than a few percent over a wide range of temperatures. Sutherland's law can be expressed as: |
:<math>\mu = \mu_{ref} \left( \frac{T}{T_{ref}} \right)^{3/2}\frac{T_{ref} + S}{T + S}</math> | :<math>\mu = \mu_{ref} \left( \frac{T}{T_{ref}} \right)^{3/2}\frac{T_{ref} + S}{T + S}</math> | ||
| Line 15: | Line 15: | ||
:<math>C_1 = \frac{\mu_{ref}}{T_{ref}^{3/2}}(T_{ref} + S)</math> | :<math>C_1 = \frac{\mu_{ref}}{T_{ref}^{3/2}}(T_{ref} + S)</math> | ||
| - | {| | + | {| border=2 |
|+ Sutherland's law coefficients: | |+ Sutherland's law coefficients: | ||
| - | ! Gas !! <math>\mu_0 [\frac{kg}{m s}]</math> !! <math>T_0 [K]</math> !! <math>S [K]</math> !! <math>C_1 [\frac{kg}{m s | + | ! Gas !! <math>\mu_0 [\frac{kg}{m s}]</math> !! <math>T_0 [K]</math> !! <math>S [K]</math> !! <math>C_1 [\frac{kg}{m s \sqrt{K}}]</math> |
|- | |- | ||
| Air | | Air | ||
Latest revision as of 04:13, 25 October 2008
In 1893 William Sutherland, an Australian physicist, published a relationship between the dynamic viscosity, 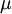 , and the absolute temperature,
, and the absolute temperature, 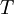 , of an ideal gas. This formula, often called Sutherland's law, is based on kinetic theory of ideal gases and an idealized intermolecular-force potential. Sutherland's law is still commonly used and most often gives fairly accurate results with an error less than a few percent over a wide range of temperatures. Sutherland's law can be expressed as:
, of an ideal gas. This formula, often called Sutherland's law, is based on kinetic theory of ideal gases and an idealized intermolecular-force potential. Sutherland's law is still commonly used and most often gives fairly accurate results with an error less than a few percent over a wide range of temperatures. Sutherland's law can be expressed as:
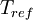 is a reference temperature.
is a reference temperature.
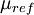 is the viscosity at the
is the viscosity at the 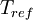 reference temperature
reference temperature
- S is the Sutherland temperature
Some authors instead express Sutherland's law in the following form:
Comparing the formulas above the 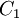 constant can be written as:
constant can be written as:
| Gas | ![\mu_0 [\frac{kg}{m s}]](/W/images/math/2/4/8/2480f45fd1c786230d032f54d5a4611f.png) | ![T_0 [K]](/W/images/math/1/e/6/1e63651a7e3249da3521fb3d1523c542.png) | ![S [K]](/W/images/math/e/4/4/e444c70ca8ff28fe00474e6ee27b3872.png) | ![C_1 [\frac{kg}{m s \sqrt{K}}]](/W/images/math/0/0/3/00379c74d249001dbd3d01bdc784a417.png)
|
|---|---|---|---|---|
| Air | 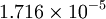
| 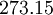
| 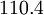
| 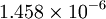
|
References
- Sutherland, W. (1893), "The viscosity of gases and molecular force", Philosophical Magazine, S. 5, 36, pp. 507-531 (1893).