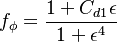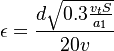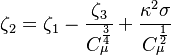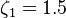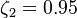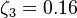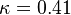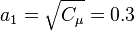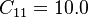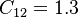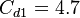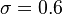Shuai-Agarwal turbulence Model
From CFD-Wiki
Introduction
One-equation k-kL turbulence model was developed from two-equation k-kL closure of Abdol-Hamid et al. [1]. Improvements to the original formulation of one-equation k-kL model (AIAA 2019-1879) were made by optimizing the model constants. The new improved model has been validated by simulating several benchmark canonical wall-bounded turbulent flows with small regions of separation from NASA TMR (https://turbmodels.larc.nasa.gov/). The model needs further investigations by the scientific community to evaluate its potential.
Shuai – Agarwal One Equation k-kL Turbulence Model
The turbulent viscosity is given by:
The final form of the new Shuai-Agarwal one-equation k-kL model is obtained as:
Where 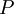 is the production term:
is the production term:
The following Bradshaw relation is used to express the relationship between 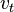 and k and kL:
and k and kL:
The parameter of the model are:
The model constants are:
References
- S. Shuai and R. K. Agarwal (2020), "A New Improved One-Equation Turbulence Model Based on k-kL Closure", AIAA Paper 2020-1075, January 2020.
- K. S. Abdol-Hamid, J. R. Carlson, and C. L. Rumsey (2016), "Verification and Validation of the k-kL Turbulence Model in FUN3D and CFL3D Codes", AIAA 2016-3941, 2016.

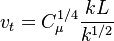
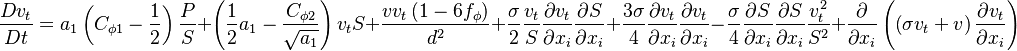
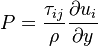
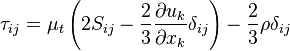
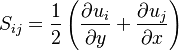
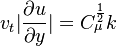
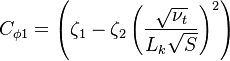
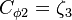
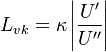

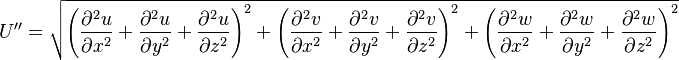
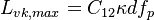
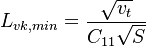
![f_{p}={min}{[max(\frac{P}{{\rho}{v_{t}}{S^{2}}} , 0.5) {,}{1.0}]}](/W/images/math/2/2/a/22a9d6e12e439928b712ce28fc78a45b.png)