SIMPLER algorithm - SIMPLE - Revised
From CFD-Wiki
m |
|||
| Line 1: | Line 1: | ||
{{stub}} | {{stub}} | ||
| + | |||
| + | The revised algorithm consist of solving the pressure equation to obtain the pressure field and solving the pressufre-correction equation only to correct the velocities. The sequence of operations can be stated as: | ||
| + | |||
| + | 1. Start with a guessed velocity field. | ||
| + | 2. Calculate the cofficients for the momentum equations and hence calculate <math>\hat{u}, \hat{v}, \hat{w} </math> from momentum equations by substituting the value of the neiboughbor velocities <math>u_{nb}</math> | ||
| + | 3. Calculate the cofficients for the pressure equation, and solve it to obtain pressure field | ||
| + | 4. Treating this pressure field as <math>p^{*}</math>, solve the momentum equation to obtain <math>u^{*},v^{*},w^{*}</math> | ||
| + | 5. Calculate the mass source <math>b</math> and hence solve the p^{'} equation | ||
| + | 6. Correct the velocity field by use, by not ''do not'' correct the pressure | ||
| + | 7. Solve the discretization equations for other <math>\varphi</math> if necessary | ||
| + | 8. Return to step 2 and repeat until convergence | ||
== References == | == References == | ||
Revision as of 12:33, 26 August 2012
The revised algorithm consist of solving the pressure equation to obtain the pressure field and solving the pressufre-correction equation only to correct the velocities. The sequence of operations can be stated as:
1. Start with a guessed velocity field.
2. Calculate the cofficients for the momentum equations and hence calculate 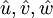 from momentum equations by substituting the value of the neiboughbor velocities
from momentum equations by substituting the value of the neiboughbor velocities 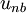 3. Calculate the cofficients for the pressure equation, and solve it to obtain pressure field
4. Treating this pressure field as
3. Calculate the cofficients for the pressure equation, and solve it to obtain pressure field
4. Treating this pressure field as 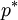 , solve the momentum equation to obtain
, solve the momentum equation to obtain 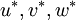 5. Calculate the mass source
5. Calculate the mass source 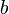 and hence solve the p^{'} equation
6. Correct the velocity field by use, by not do not correct the pressure
7. Solve the discretization equations for other
and hence solve the p^{'} equation
6. Correct the velocity field by use, by not do not correct the pressure
7. Solve the discretization equations for other 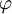 if necessary
8. Return to step 2 and repeat until convergence
if necessary
8. Return to step 2 and repeat until convergence
References
- Patankar, S.V. (1980), Numerical Heat Transfer and Fluid Flow, Hemisphere Publishing Corporation, Taylor & Francis Group, New York. ISBN-13: 978-0891165223.
Return to Numerical Methods
