 |
|
|
[Sponsors] | |||||
Linear decay - implementation and convergence issues |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Andrea Di Ronco
Join Date: Nov 2016
Location: Milano, Italy
Posts: 57
Rep Power: 10  |
Hello,
one of the custom solvers I'm working on features some simple steady-state transport equations of the form  where 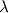 is a uniform linear decay constant, is a uniform linear decay constant, 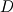 is an effective diffusivity which can depend on temperature and the flow field, and is an effective diffusivity which can depend on temperature and the flow field, and 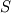 is a volumetric source term which also has a complex dependence on other fields. is a volumetric source term which also has a complex dependence on other fields.The equation is simply implemented as Code:
fvScalarMatrix cEqn
(
fvm::div(phi, c)
- fvm::laplacian(D, c)
+ fvm::Sp(lambda, c)
==
S
);
 . .In particular, physical meaning (radioactive decay) imposes very small values (e.g. of the order of 1e-5/1e-8 s^-1), for which convergence is unacceptably slow. I recognise this can be a reasonable behaviour, but I'd like to understand a little bit more. In particular, from the implemented equation is clear (to me) that when all other quantities reach numerical convergence, the equation becomes fully implicit in  since coupling with other equations acts only in one way. The test cases are actually simple, with fully orthogonal meshes. since coupling with other equations acts only in one way. The test cases are actually simple, with fully orthogonal meshes.Shouldn't the equation be solved "exactly" when other fields become fixed after convergence? Or is it maybe just a matter of how residuals are defined, and the fact that residuals take forever to lower doesn't affect the actual solution? I feel like I'm missing something, so any suggestion would be greatly appreciated  Andrea |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Temperature convergence problem with nonsmooth thermal conductivity | bmercer | OpenFOAM Running, Solving & CFD | 4 | November 14, 2017 14:25 |
| false time step implementation for steady state | Kushagra | CFX | 1 | June 22, 2008 20:06 |