 |
|
|
[Sponsors] | |||||
3D vortex panel method - wing tip and Kutta problems with elliptic wing |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Pedro de Almeida Secchi
Join Date: Feb 2020
Posts: 11
Rep Power: 6  |
Hi!
I've assembled my own 3D vortex panel method code through the methodology presented at http://www.dept.aoe.vt.edu/~devenpor...l%20Method.pdf, which has succeeded in calculating the supperficial velocity accross a sphere in the manner presented in the pdf at hand (i. e. using vortex rings as singularity elements with the neumann condition applied to collocation points at the center of each panel. I've tried to extend it to lifting bodies using a trailing edge vortex ring (equivalent to the wake doublet sheet proposed by Katz and Plotkin - chapter 12 of Low Speed Aerodynamics, first order 3D panel methods) with vorticity equal to the difference between the lower and upper TE panels, separated by a small gap. I've failed, however, in simulating an elliptical NACA-0012 wing at 5 deg. AOA. I've gathered plotted results here: https://drive.google.com/drive/folde...Xf?usp=sharing Plotting the superficial velocity vectors at the surface (elliptic test.png, elliptic anomally closeup.png) we can see an abrupt increase in superficial velocity ate the wing tip. I've tried refining the mesh and using a cosinoidal panel distribution so as to improve mesh quality at the tip, yet the error persisted and even increased in intensity (see elliptic lift distribution.png, a Cl/y graph, and its cosinoidal mesh counterpart). The elliptic distributions I gathered seem to be "right-ish", with an approximately constant Cl throughout the wing, in spite of the tip annomally. However, I've plotted a circulation per panel x-y position scattergram throughout the wing to check wether my mistake could have been generated by the use of finite difference method to compute local velocity at the small tip panels (which would generate relatively big numerical imprecisions) and arrived at the scattergram in "elliptic scattergram circulation.png". As you can see there, the circulations on upper (orange) and lower (blue) surfaces tend to an equal value at the trailing edge, leading to a value of zero circullation at the wake vortexes. That probably led to a stagnation point out of the TE, too, with Kutta condition being violated. Am I doing any conceptual mistakes while applying Kutta condition to the trailing edge? I've used an approximately infinite wake vortex ring (offset by 3000 times the chord in the streamwise direction) instead of a horseshoe vortex so as to make it easier to later adapt the code for different wake geometries, e. g. with several queued wake vortex rings. The function to generate their respective AICs and adding them to the TE panels's positions at the AIC matrix is apparently being correctly ran, as I have verified directly checking the matrix. Is the TE horseshoe vortex with circullation equal to the difference between upper and lower TE panels enough to apply Kutta condition when using Neumann contour conditions instead of the more commonly used Dirichlet conditions? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
|
I'm not sure, but from your description it seems that you are using just 1 single vortex ring for the wake of the whole wing, instead of 1 for each couple of panels meeting at the trailing edge. If this is the case, this is completely wrong and not expected to give any useful result.
Moreover, it is not clear what you mean by vorticity equal to the difference between the lower and upper TE panels, separated by a small gap. There should be no gap at all between the panels (except for the singularity issue in this method, that I mentioned in another post, which requires removing one equation/panel per closed body). In addition, Kutta condition has to be part of the equations. So if you solve the system correctly (I suggest you to check that by computing the residual), it is necessarily satisfied if it is part of the equations. In this method the Kutta condition is usually implemented by modifying the coefficients of the two panels meeting at the trailing edge (or at any other line where a vortex sheet is assumed to be released in the flow). May I also ask how did you implement the self-induced velocity part due to the gradient of the Gamma on the surface? How do you handle the high curvature regions? Do you actually split the wing surface in multiple patches and apply the method separately, say, on the lower and upper surface? Because the method presented in the slides above would surely fail when applied across the tip of the wing, not to mention the trailing edge (where, actually, you should consider the wake panel). Finally, have you actually taken into account the singularity issue I mentioned in the other post? May I also suggest to start with a 0 degree case of a wing with a symmetric profile (elliptic or not)? |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Pedro de Almeida Secchi
Join Date: Feb 2020
Posts: 11
Rep Power: 6  |
I'm using one wake vortex ring per trailing edge panel, not a single wake ring.
I've reprogrammed the surface gradient computation for something like: * Used a rectangular (mxn panels) mesh, defining  and and 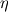 coordinates which vary from 0 to 1 respectively along the m rows and the n columns of panels in the mesh; coordinates which vary from 0 to 1 respectively along the m rows and the n columns of panels in the mesh;* Derived  by by  and and 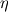 ; ;* Computed  , ,  and other cartesian coordinate derivatives along the surface; and other cartesian coordinate derivatives along the surface;* Determined the surface gradient as the solution for the system: Code:
lg.solve(np.vstack((np.array([[dxdxi[i, j], dydxi[i, j], dzdxi[i, j]], \
[dxdeta[i, j], dydeta[i, j], dzdeta[i, j]]]), nvectmat[i, j, :])), \
np.array([dwdxi[i, j], dwdeta[i, j], 0.0]))
 , ,  values along the surface and is normal to it. values along the surface and is normal to it.Surface gradient calculations seem to be right, and have worked appropriately both for my sphere test case and the 0 AOA NACA 0012 case, disregarding wake AICs - so, for non-lifting cases. I've now switched for a straight wing with a NACA 4412 airfoil, without any trailing edge gap. The high-curvature problem I was having with the elliptic wing tip is no longer an issue, but yet I've been reaching extremely high trailing edge Cps and velocities thanks to how the calculated  s quickly vary to equal values at the trailing edge, as in the attached plot. I've checked and the computed surface gradient also jumps to an absurdly high value close to the TE thanks to that quick variation. s quickly vary to equal values at the trailing edge, as in the attached plot. I've checked and the computed surface gradient also jumps to an absurdly high value close to the TE thanks to that quick variation.Plus, velocities at the last upper and lower panels do not match, so Kutta condition is not being reinforced by the trailig edge vortex, though its AIC is being calculated in exactly the same fashion as that of any other panel and its geometry is correct. Even though, all velocity vectors are normal to the surface, so at least Neumann condition is being respected and the linear system is being correctly solved. Plus, I couldn't find a freely available pdf for Srivastava's paper the Bangalore institute's page says its only available for repository staff: https://nal-ir.nal.res.in/1726/ |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Pedro de Almeida Secchi
Join Date: Feb 2020
Posts: 11
Rep Power: 6  |
Sorry, I forgot to attach this file ( circulation plot at the TE) when writting my last reply.
|
|
|
|

|
|
|
|
|
#6 |
|
New Member
Pedro de Almeida Secchi
Join Date: Feb 2020
Posts: 11
Rep Power: 6  |
My e-mail is pedro.secchi@ga.ita.br
|
|
|
|

|
|
|
|
|
#8 |
|
New Member
Pedro de Almeida Secchi
Join Date: Feb 2020
Posts: 11
Rep Power: 6  |
I've managed to fix the code reprogramming it according to Ashok Srivastava's approach, which Paolo has presented me to.
Srivastava calculated the surface gradient of panel vorticity based in its value not at adjacent panel collocation points, as I have, but based on each adjacent vortex line segment and its resultant vortex strength, as in:  In which G stands for local vorticity, s is a vortex line segment vector, Gamma is the line segment's strength, n is the panel's normal vector and N is the amount of sides the panel possesses. This individual vortex line approach also allowed me to correct the computation of trailing edge local velocities, and computing the AIC coefficients of each individual vortex line to later add 'em up into panel AICs has also aided me in speeding up calculations. Basically, my code was calculating vorticity right. Yet, my surf. gradient calculation did not consider the shared edge between upper and lower TE panels, which were located at oposite edges of the grid I've mentioned before. Thus AIC and vorticity calculations got the AICs for that panel correctly as panel+wake panel, leading to no resultant consideration of the trailing edge vortex line segment; yet surface gradients did not, and considered the TE vortex's strength as the panel's own vorticity without adding that which was due to the adjacent TE panel or the wake panel. And that was why Kutta condition was not regarded, in spite of a wake panel having been added. |
|
|
|

|
|
|
|
|
#9 |
|
New Member
C. Han
Join Date: Feb 2020
Posts: 7
Rep Power: 6  |
Hello. It was more than 20 years ago when I read a paper by Ashok Srivastava and Dean T. Mook published by AIAA J. of Aircraft.
At that time, I also tried to solve a sphere problem using vortex ring elements. The redundancy in the matrix was cured by using several techniques. The final problem left was to calculate the surface velocity. At that time I contacted the Ashok Srivastava and he gave me the answer via email which I do not have today. Last year I tried to solve the body of revolution using the same method, and I found that I have the simple code which did not exactly match with the theory. I could not find what I was wrong at that time. I am wondering if one of you can send the Ashok Srivastava's paper or his approach. My email address is : chhan@ut.ac.kr |
|
|
|

|
|
|
|
|
#10 |
|
New Member
Pedro de Almeida Secchi
Join Date: Feb 2020
Posts: 11
Rep Power: 6  |
Hi, I've just emailed you the papers you've asked for.
Good luck! Just to mention something else which might help with your debugging, Srivastava mentioned in his appendix the equation  Which hasn't worked for me. Instead, resorting to  Has given me the correct surface gradient, as I mentioned above. Perhaps this is due to some mistake I have made, but in case it's not, it might help you in your debugging. |
|
|
|

|
|
|
|
|
#11 |
|
New Member
Pedro de Almeida Secchi
Join Date: Feb 2020
Posts: 11
Rep Power: 6  |
Here are also some previous threads that helped me and Paolo with surface velocity in non-lifting cases:
3D PANEL METHOD Panel-Method, velocity calculation There's also http://www.dept.aoe.vt.edu/~devenpor...l%20Method.pdf Which also handles bodies of revolution. |
|
|
|

|
|
|
|
|
#12 |
|
New Member
C. Han
Join Date: Feb 2020
Posts: 7
Rep Power: 6  |
Thanks for the files.
I found that I did use -grad G/2=\Sigma s_i \Gamma_i X n/4\pi, long time ago. In the stagnation point, triangular element can lead some error if the correct tangential and normal unit vectors are assigned at those elements. |
|
|
|

|
|
 |
|
|