 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Hanniel Freitas
Join Date: Jan 2012
Location: Natal, Brazil
Posts: 34
Rep Power: 14  |
Hi Foamers!
I'm having a little bit of trouble trying to remake the work done at the work of Waheed et al (2002) (http://www.sciencedirect.com/science...17931002001242), where some axissymetric wedge section of a drop inside a cilinder is taken, this drop containing solute, and the outer phase is solute-free. So, essencially I want to computate the solute transfer. The main problem is that i need to establish a equilibrium of the solute concentration inside and outside the drop, what I believe I could do by phisically stablishing a interface boundary in my domain and using groovyBC to ser the dragient expression. So, essencially, my domain would consist of 2 regions: the drop and the outer phase. By now, the mesh construction is OK, and I could stablish this phisical boundary and the paraFoam recognizes it. But running my case in my own implementation of interfoam (interfoam + solute transport), i noticed that the interface bondary (so called defaultFaces) is not needed. In fact, I can remove it from the boundary listed in the 0 directory with no problem! That's not right, my solver just ignores my equilibrium condition. What should I do? My master depends on this series of simulation  I'm attaching my case files. Thanks in advance, I hope someone out there could help me. PS: In order to save space, after download and extraction please run blockMesh. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Anton Kidess
Join Date: May 2009
Location: Germany
Posts: 1,377
Rep Power: 30  |
I think you need two domains with non-identical vertices, which you then couple using some sort of a baffle boundary condition. Have a look at the tutorials for chtMultiRegionFoam, where this is done for the temperature equation.
- Anton
__________________
*On twitter @akidTwit *Spend as much time formulating your questions as you expect people to spend on their answer. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Cyprien
Join Date: Feb 2010
Location: Stanford University
Posts: 299
Rep Power: 18  |
Do you have a partitioning relationship between the concentration in both side of the interface ?
Something like :  If it is the case, you can add a transport equation in interFoam solver using the theory of distributions (see Haroun (2012) for exemple)). The concentration jump will be considered as an additional term in your transport equation. Best, Cyp Last edited by Cyp; November 19, 2012 at 09:27. |
|
|
|

|
|
|
|
|
#4 |
|
Member
Hanniel Freitas
Join Date: Jan 2012
Location: Natal, Brazil
Posts: 34
Rep Power: 14  |
Dear Cyp and Anton,
Thanks for the fast reply. I will check your suggetions, thanks in advance. And yes Cyp, i have a partitioning condition like the one you showed. But how could I implement this on the solver to consider this jump only thru the interface boundary? I will check the reference you suggested. |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Cyprien
Join Date: Feb 2010
Location: Stanford University
Posts: 299
Rep Power: 18  |
I can explain it to you through a simple example. Consider only the diffusion between two phases (beta and gamma for instance) :
In the beta-phase you have  and in the gamma-phase  Both phases are connected through a flux continuity at the interface  and the thermodynamic equilibrium condition reads:  What you look for is an partial differential equation that govern  where 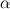 is the phase indicator provided from the VOF solution. With such a formulation, C is defined on the whole domain. In the same manner, you can defined a diffusion field as is the phase indicator provided from the VOF solution. With such a formulation, C is defined on the whole domain. In the same manner, you can defined a diffusion field as  Now you express the derivative of C :  multiplying this relation by D and applying the divergence operator, you get :   Just keep in mind that according to the distribution theory you have :  . Consequently, the previous equation reduces to: . Consequently, the previous equation reduces to: This additional term represents the interfacial jump condition. If there is a continuity, you can get rid of it. However, if you have a partitioning relation, you have to consider it. At the interface, we have  . .Consequently,  more over,  So  So your diffusion equation becomes :  With such a formulation, you will automaticly have a jump condition at the interface between beta and gamma. You can also optimised the solution with  I let you adapt this exemple to the advection-diffusion equation. Best regards, Cyp Last edited by Cyp; November 19, 2012 at 09:26. |
|
|
|

|
|
|
|
|
#6 | |
|
Member
Luca Giannelli
Join Date: Jun 2010
Location: Kobe, Japan
Posts: 58
Rep Power: 16  |
Quote:
I don't actually know if you are still following this tread but I have a couple of questions. It came for me too the time to implement the phase jump condition so I came back to this useful thread. In my previous case (a non-volatile tracer) I just had the Laplacian of a bunch of constants and alpha1: no problem in the solution if you insert the explicit laplacian (alpha1 already calculated). But in this case it is different because we have C an alpha1 simultaneously in the laplacian. For what I can see in the other terms OpenFOAM always expects in the laplacian a dimensionedScalar and a volScalarField. So, I gathered all the constant terms in the fraction and calculated them before the C equation:  Being this a function of alpha1 I had to define it in the Createfields.H as another volScalarField. Again, no problem. What I actually cannot understand is: how do I formulate this in C++??  should become Code:
fvm::laplacian(DC, C) Moreover my low C++ knowledge prevents me for finding an alternative formulation. Do you have any hint? Thanks! |
||
|
|

|
||
|
|
|
#7 | |
|
New Member
Rimsha
Join Date: Jan 2016
Posts: 25
Rep Power: 10  |
Quote:
Kind Regards Rimsha |
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Cyprien
Join Date: Feb 2010
Location: Stanford University
Posts: 299
Rep Power: 18  |
@Article{Haroun2010,
Title = {Volume of fluid method for interfacial reactive mass transfer: Application to stable liquid film }, Author = {Y. Haroun and D. Legendre and L. Raynal}, Journal = {Chemical Engineering Science }, Year = {2010}, Number = {10}, Pages = {2896 - 2909}, Volume = {65}, Abstract = {A volume of fluid method is developed in order to simulate reactive mass transfer in two-phase flows and is applied to study reactive laminar liquid film. The thermodynamic equilibrium of chemical species at the interface is considered using Henry's law. The chemical species concentration equation is solved using primitive variables and local fluxes are locally directly calculated at the interface. The present treatment of jump discontinuity of chemical concentration is consistent with a volume of fluid approach and the difficulty to calculate accurate local mass flux across interface is overcome. For plane interface, the precision of the numerical simulation is found to be very satisfactory while for curved interface a special procedure has been developed to reduce the development of spurious fluxes at the interface. The algorithm is validated for different cases by comparison with available solutions. The method is then applied to study non-reactive and reactive mass transfer in a falling liquid film. The results show that the liquid side mass transfer is well predicted by the Higbie (1935) theory when the transfer is controlled by the film advection provided that adequate parameters are considered, i.e. the actual velocity at interface and not the average liquid film velocity. For situations controlled by diffusion, the Sherwood number tends to a constant value characteristic of purely diffusive situations. For the reactive mass transfer, first and second order irreversible chemical reactions in the liquid phase are considered. The numerical results are compared respectively, with Danckwerts (1970) and Brian et al. (1961) solutions and good agreement is observed. The proposed Volume of Fluid method is shown to be well adapted to deal with interfacial reactive mass transfer problems. }, DOI = {http://dx.doi.org/10.1016/j.ces.2010.01.012}, File = {Haroun2010.pdf:ARTICLES/Haroun2010.pdf:PDF}, ISSN = {0009-2509}, Keywords = {\{CFD\}}, URL = {http://www.sciencedirect.com/science/article/pii/S0009250910000291} } Cheers, |
|
|
|

|
|
|
|
|
#9 | |
|
New Member
Rimsha
Join Date: Jan 2016
Posts: 25
Rep Power: 10  |
Quote:
Rimsha |
||
|
|

|
||
|
|
|
#10 |
|
Member
Timm Severin
Join Date: Mar 2014
Location: Munich
Posts: 63
Rep Power: 12  |
Note that although it was ages ago there is a mistake in the derivation done by Cyp:
is wrong, it should be  leading to the result of  which, by the way, describes the view from "the other phase" compared to Haroun, who ends up at  which would be equal to assuming  (which in fact is just (which in fact is just  ). ).Note that Cyps answer was a mixup of both solutions of nominator and denominator. Edit: Thanks anyway Cyp, this was generally a great help. And while at it, has anyone here managed to reproduce the calculations in the paper with OpenFOAM? I kind of struggle with different Henry coefficients (some work, some produce an exception). |
|
|
|

|
|
|
|
|
#11 |
|
Member
Timm Severin
Join Date: Mar 2014
Location: Munich
Posts: 63
Rep Power: 12  |
Finally my solver works now the way it was supposed to be. For anyone who cares I will attach my modified solver as well as two testcases. All modifications were made by made, but based on the publication by Haroun et al (2010), cited above, as well as Nieves-Remacha et al (2015):
OpenFOAM Computational Fluid Dynamic Simulations of Two-Phase Flow and Mass Transfer in an Advanced-Flow ReactorThe Attachements: interHarounFoam: This is the solver. it is a modified version of interFoam, implementing both Equations found in Nieves-Remacha (2015), Supplemental. This means it implements as well the Haroun approach, as an approach by Marshall et al. (2012). It is merely for testing purpose, the diffusion coefficients are fixed toNievesRemacha2015: This is a sample case for the first example in the supplemental by Nieves-Remacha et al. It contains all relevant data to run interHarounFoam and generate one set of the results.Haroun2010: A sample case to reproduce the example shown in Figure 1 a/b of Haroun et al. (2010). This case can be run as it is, too.A couple of further notes:
May the foam be with you, Timm |
|
|
|

|
|
|
|
|
#12 |
|
New Member
Join Date: Jan 2016
Posts: 10
Rep Power: 10  |
Hello,
I don't know if anyone is still following this conversation but I have a question concerning the harmonic averaging of the diffusivity as it is mentioned in Haroun et al. (2010): As I know, the harmonic averaging is usually performed with a factor 2. So does anyone know why in this case it is  instead of  I would be very glad if you could help me out with this. Thanks and best regards! Katharina |
|
|
|

|
|
|
|
|
#13 |
|
Member
Timm Severin
Join Date: Mar 2014
Location: Munich
Posts: 63
Rep Power: 12  |
I'm not sure how the harmonic mean is derived exactly, but if you look at wikipedia, there is a definition for the weighted harmonic mean:
 which you can rewrite for the harmonic function given. Apart from that, simple calculation would show you that a factor of two leads to invalid results, as 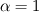 or or  will lead the the corresponding diffusion coefficient twice as big as it should be in the pure phase. will lead the the corresponding diffusion coefficient twice as big as it should be in the pure phase.
|
|
|
|

|
|
|
|
|
#14 |
|
New Member
Join Date: Jan 2016
Posts: 10
Rep Power: 10  |
Thank you so much for the quick reply, Astrodan. Especially your last sentence makes it very clear why there is no need for an additional factor.
|
|
|
|

|
|
|
|
|
#15 |
|
New Member
Join Date: Jan 2016
Posts: 10
Rep Power: 10  |
Sorry, I have to ask another thing:
So, the equation  is a substitute for the usual linear average of the diffusion:  If we have  for gas and for gas and 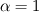 for liquid, the usual linear averaging leads to for liquid, the usual linear averaging leads to for for 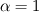 and and  for for  . .However, if I use the harmonic averaging, I get:  for for  : : and  for for 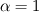 . .Am I getting this wrong and making a mistake somewhere? Shouldn't the result be the same for the case of pure phases? |
|
|
|

|
|
|
|
|
#16 |
|
Member
Phanindra
Join Date: Jan 2013
Posts: 39
Rep Power: 13  |
Hi Adrean,
I have implemented your equation and was able to get the concentration distribution for 1D diffusional problem which was matching exactly with Analytical solution. But when I try to calculate the fluxes. I'm getting very high values as a result my Mass transfer coefficient valuations are wrong. can you please brief me, how did you calculate the fluxes across interface? My code is as attached in the attachment.......also you can have a look at the C profile from the picture attached Eagerly waiting for your reply |
|
|
|

|
|
|
|
|
#17 | |
|
New Member
jawfi
Join Date: Sep 2017
Posts: 3
Rep Power: 9  |
Quote:
Hi Timm, Sorry but how can I open the modified solvers you attached ? I am interested to use these equations and modify them but I wasn't able to load cases with your modified solvers ? your help is appreciated ! Thanks, |
||
|
|

|
||
|
|
|
#18 |
|
Member
Join Date: May 2017
Posts: 44
Rep Power: 9  |
Dear Foamer,
I am going to use the same approach for the multiphase case. Any idea about the mass flux? Thanks, |
|
|
|

|
|
|
|
|
#19 | ||
|
Member
Timm Severin
Join Date: Mar 2014
Location: Munich
Posts: 63
Rep Power: 12  |
Quote:
Quote:
I think that for some meshes a high flux might occur simply due to numerical interpolation errors at the mesh points in immediate vicinity of the interface. Check that, too. Well, tell us what you got so far, what fails, and where your problem is exactly. No one can answer based on a question like that. Apart from that, check the source papers and above posts.. |
|||
|
|

|
|||
|
|
|
#20 |
|
Member
Join Date: May 2017
Posts: 44
Rep Power: 9  |
Hi Foamers,
I have the transport equation for concentration which is validated with the analytical solution. Now I am trying to add phase change through Sp and Su. I used CEqn.flux() and add that term as Su and Sp to alphaEqn.H but it didn't work. Any idea how I should solve this problem with phase change. Thanks, Bita |
|
|
|

|
|
 |
| Tags |
| drop, interface position, interfoam, openfoam |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Wind turbine simulation | Saturn | CFX | 60 | July 17, 2024 06:45 |
| An error has occurred in cfx5solve: | volo87 | CFX | 5 | June 14, 2013 18:44 |
| RPM in Wind Turbine | Pankaj | CFX | 9 | November 23, 2009 05:05 |
| Convective Heat Transfer - Heat Exchanger | Mark | CFX | 6 | November 15, 2004 16:55 |
| Replace periodic by inlet-outlet pair | lego | CFX | 3 | November 5, 2002 21:09 |